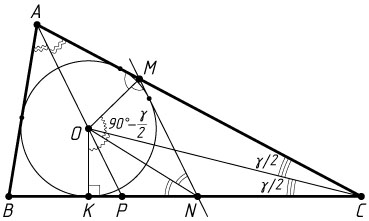
11219. Окружность с центром O
, вписанная в треугольник ABC
, касается стороны BC
в точке K
. К этой окружности проведена касательная, параллельная биссектрисе AP
треугольника и пересекающая стороны AC
и BC
в точках M
и N
соответственно.
а) Докажите, что угол MOC
равен углу NOK
.
б) Найдите периметр треугольника ABC
, если отношение площадей трапеции AMNP
и треугольника ABC
равно 2:7
, MN=2
, AM+PN=6
.
Ответ. 28.
Решение. а) Обозначим \angle ACB=\gamma
. Центр окружности, вписанной в угол, лежит на его биссектрисе. Тогда \angle MON=90^{\circ}-\frac{\gamma}{2}
как угол между биссектрисами внешних углов треугольника MCN
(см. задачу 4770). С другой стороны, из прямоугольного треугольника CKO
получаем, что \angle COK=90^{\circ}-\frac{\gamma}{2}
, значит, \angle MON=\angle COK
. Следовательно,
\angle MOC=\angle MON-\angle CON=\angle COK-\angle CON=\angle NOK.
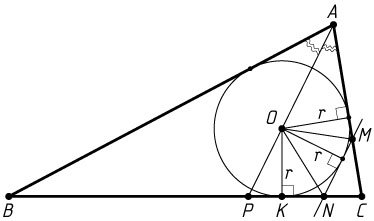
б) Пусть радиус вписанной окружности треугольника ABC
равен r
, а периметр треугольника ABC
равен 2p
. Тогда
S_{AMNP}=S_{\triangle AOM}+S_{\triangle MON}+S_{\triangle NOP}=\frac{1}{2}AM\cdot r+\frac{1}{2}MN\cdot r+\frac{1}{2}NP\cdot r=
=\frac{1}{2}r(AM+MN+NP)=\frac{1}{2}r(6+2)=4r,
S_{\triangle ABC}=pr
(см. задачу 452). Следовательно,
\frac{2}{7}=\frac{S_{AMNP}}{S_{\triangle ABC}}=\frac{4r}{pr}=\frac{4}{p},
откуда 2p=28
.
Источник: Диагностические и тренировочные задачи ЕГЭ. — 2019

