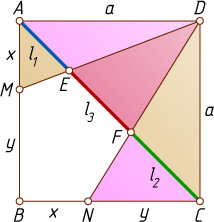
11395. На сторонах AB
и BC
квадрата ABCD
взяты такие две точки M
и N
, что BM+BN=AB
. Докажите, что прямые DM
и DN
делят диагональ AC
на три отрезка, из которых можно составить треугольник, причём один угол этого треугольника равен 60^{\circ}
.
Решение. Первый способ. Пусть отрезки DM
и DN
пересекают диагональ AC
в точках E
и F
соответственно. Обозначим AB=a
, AM=x
, CN=y
. Тогда x+y=a
.
Отрезки AE
и CF
— биссектрисы прямоугольных треугольников DAM
и CDN
, поэтому
l_{1}=AE=\frac{2AD\cdot AM\cos45^{\circ}}{AD+AM}=\frac{ax\sqrt{2}}{a+x},~l_{2}=CF=\frac{2CD\cdot CN\cos45^{\circ}}{CD+CN}=\frac{ay\sqrt{2}}{a+y}
(см. задачу 4021). Тогда
l_{3}=EF=AC-l_{1}-l_{2}=a\sqrt{2}-\frac{ax\sqrt{2}}{a+x}-\frac{ay\sqrt{2}}{a+y}=
=a\sqrt{2}\left(1-\frac{x}{a+x}-\frac{y}{a+y}\right)=\frac{a\sqrt{2}(a^{2}-xy)}{(a+x)(a+y)}.
Значит,
l_{1}+l_{2}\gt l_{3}~\Leftrightarrow~\frac{ax\sqrt{2}}{a+x}+\frac{ay\sqrt{2}}{a+y}\gt\frac{a\sqrt{2}(a^{2}-xy)}{(a+x)(a+y)}~\Leftrightarrow
\Leftrightarrow~\frac{x}{a+x}+\frac{y}{a+y}\gt\frac{a^{2}-xy}{(a+x)(a+y)}~\Leftrightarrow~ax+xy+ay+xy\gt a^{2}-xy~\Leftrightarrow
\Leftrightarrow~a(x+y)+2xy\gt a^{2}-xy~\Leftrightarrow~a^{2}+3xy\gt a^{2}~\Leftrightarrow~xy\gt0.
Последнее неравенство очевидно. Далее
l_{1}+l_{3}\gt l_{2}~\Leftrightarrow~\frac{ax\sqrt{2}}{a+x}+\frac{a\sqrt{2}(a^{2}-xy)}{(a+x)(a+y)}\gt\frac{ay\sqrt{2}}{a+y}~\Leftrightarrow
\Leftrightarrow~\frac{y}{a+y}-\frac{x}{a+x}\lt\frac{a^{2}-xy}{(a+x)(a+y)}~\Leftrightarrow~ay+xy-ax-xy\lt a^{2}-xy~\Leftrightarrow
\Leftrightarrow~a(y-x)\lt a^{2}-xy~\Leftrightarrow~(x+y)(y-x)\lt(x+y)^{2}-xy~\Leftrightarrow
\Leftrightarrow~y^{2}-x^{2}\lt x^{2}+y^{2}+xy~\Leftrightarrow~2x^{2}+xy\gt0.
Последнее неравенство очевидно. Аналогично, l_{2}+l_{3}\gt l_{1}
. Следовательно, из отрезков l_{1}
, l_{2}
, l_{3}
можно составить треугольник.
Докажем, что косинус угла \alpha
, противолежащего стороне, равной l_{3}
, равен \frac{1}{2}
. Действительно,
\cos\alpha=\frac{l_{1}^{2}+l_{2}^{2}-l_{3}^{2}}{2l_{1}l_{2}}=\frac{\frac{2a^{2}x^{2}}{(a+x)^{2}}+\frac{2a^{2}y^{2}}{(a+y)^{2}}-\frac{2a^{2}(a^{2}-xy)^{2}}{(a+x)^{2}(a+y)^{2}}}{2\cdot\frac{ax\sqrt{2}}{a+x}\cdot\frac{ay\sqrt{2}}{a+y}}=
=\frac{\frac{x^{2}}{(a+x)^{2}}+\frac{y^{2}}{(a+y)^{2}}-\frac{(a^{2}-xy)^{2}}{(a+x)^{2}(a+y)^{2}}}{\frac{2xy}{(a+x)(a+y)}}=\frac{x^{2}(a+y)^{2}+y^{2}(a+x)^{2}-(a^{2}-xy)^{2}}{2xy(a+x)(a+y)}=
=\frac{x^{2}a^{2}+2axy(x+y)+x^{2}y^{2}+a^{2}y^{2}-a^{4}+2a^{2}xy}{2xy(a+x)(a+y)}=
=\frac{x^{2}a^{2}+2a^{2}xy+x^{2}y^{2}+a^{2}y^{2}-a^{4}+2a^{2}xy}{2xy(a+x)(a+y)}=
=\frac{a^{2}(x^{2}+2xy+y^{2})+x^{2}y^{2}-a^{4}+2a^{2}xy}{2xy(a+x)(a+y)}=\frac{a^{4}+x^{2}y^{2}-a^{4}+2a^{2}xy}{2xy(a+x)(a+y)}=
=\frac{xy(xy+2a^{2})}{2xy(a^{2}+a(x+y)+xy)}=\frac{(xy+2a^{2})}{2(a^{2}+a^{2}+xy)}=\frac{xy+2a^{2}}{2(2a^{2}+xy)}=\frac{1}{2}.
Следовательно, \alpha=60^{\circ}
. Что и требовалось доказать.
Второй способ. Легко проверить, что
l_{3}^{2}=l_{1}^{2}+l_{2}^{2}-l_{1}l_{2}.
Из этого равенства (и теоремы косинусов) следует, что треугольник со сторонами l_{1}
, l_{2}
и l_{3}
существует, и угол, противоположный его стороне l_{3}
, равен 60^{\circ}
.
Третий способ. Пусть отрезки DM
и DN
пересекают диагональ AC
в точках E
и F
соответственно. Обозначим AB=a
, AM=x
, CN=y
, AE=l_{1}
, CF=l_{2}
, EF=l_{3}
. Тогда x+y=a
.
Из подобия треугольников AME
и CDE
получаем
\frac{l_{1}}{l_{2}+l_{3}}=\frac{AE}{CE}=\frac{AM}{CD}=\frac{x}{a},
а из подобия треугольников CNF
и ADF
—
\frac{l_{2}}{l_{1}+l_{3}}=\frac{CF}{AF}=\frac{CN}{AD}=\frac{y}{a}.
Значит,
\frac{l_{1}}{l_{2}+l_{3}}+\frac{l_{2}}{l_{1}+l_{3}}=\frac{x+y}{a}=1,
откуда
l_{1}(l_{1}+l_{3})+l_{2}(l_{2}+l_{3})=(l_{1}+l_{3})(l_{2}+l_{3})~\Leftrightarrow~l_{1}^{2}+l_{2}^{2}-l_{1}l_{2}=l_{3}^{2}.
Из полученного равенства и теоремы косинусов следует, что существует треугольник со сторонами l_{1}
, l_{2}
, l_{3}
, причём угол против стороны l_{3}
равен 60^{\circ}
.
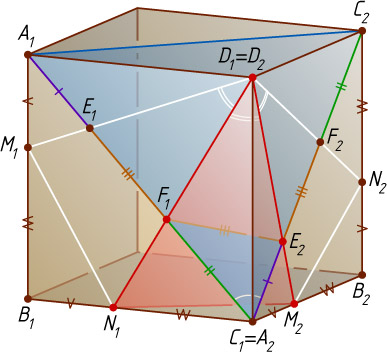
Четвёртый способ. (Выход в пространство.) Пусть отрезки DM
и DN
пересекают диагональ AC
в точках E
и F
соответственно. Поместим две копии чертежа на соседние грани куба, как показано на рисунке. Прямоугольные треугольники M_{1}B_{1}N_{1}
, M_{2}B_{2}N_{2}
и N_{1}C_{1}M_{2}
равны по двум катетам. Значит, M_{1}N_{1}=N_{1}M_{2}=N_{2}M_{2}
. А поскольку D_{1}M_{1}=D_{1}M_{2}
и D_{1}N_{1}=D_{1}N_{2}
, то по трём сторонам равны и треугольники M_{1}N_{1}D_{1}
, M_{2}N_{2}D_{1}
и M_{2}N_{1}D_{1}
. Следовательно, \angle M_{1}D_{1}N_{1}=\angle M_{2}D_{1}N_{2}=\angle N_{1}D_{1}M_{2}
. Так как D_{1}E_{1}=D_{1}E_{2}
и D_{1}F_{1}=D_{1}F_{2}
, то по двум сторонам и углу между ними равны треугольники E_{1}D_{1}F_{1}
, E_{2}D_{1}F_{2}
и E_{2}D_{1}F_{1}
. Поэтому E_{1}F_{1}=E_{2}F_{2}=F_{1}E_{2}
. Треугольник C_{1}F_{1}E_{2}
составлен из отрезков, на которые разбита диагональ исходного квадрата. Причём его угол при вершине C_{1}
равен углу A_{1}C_{1}C_{2}
сечения куба, равному 60^{\circ}
(A_{1}C_{1}C_{2}
— равносторонний треугольник).
Пятый способ. Пусть отрезки DM
и DN
пересекают диагональ AC
в точках E
и F
соответственно.
Рассмотрим преобразование f
сжатия к прямой AC
с коэффициентом k=\frac{1}{\sqrt{3}}
, т. е. преобразование, переводящее точку Z
в такую точку Z'
на прямой, перпендикулярной AC
, что \rho(Z',AC)=k\cdot\rho(Z,AC)
. Заметим, что прямую, пересекающую прямую AC
, преобразование f
переводит в прямую, пересекающую AC
в той же точке.
Обозначим X=f(B)
, Y=f(D)
. Тогда AXY
и CXY
— равносторонние треугольники. Пусть P=f(M)
, Q=F(N)
, Q'=F(N')
, где N'
— точка, симметричная N
относительно BD
(точка Q'
симметрична Q
относительно BD
, кроме того, BN'=BN=AM
). Поскольку MP\parallel N'Q'\parallel BD
, по теореме Фалеса из равенства AM=BN'
следует, что AP=XQ'
, а из симметрии XQ'=XQ
; значит, AP=XQ
. Так как треугольники AXY
и CXY
равносторонние, из этого следует равенство треугольников APY
и XQY
. Следовательно, \angle EYF=\angle PYQ=60^{\circ}
, поскольку f(DM)=YP
и f(DN)=YQ
.
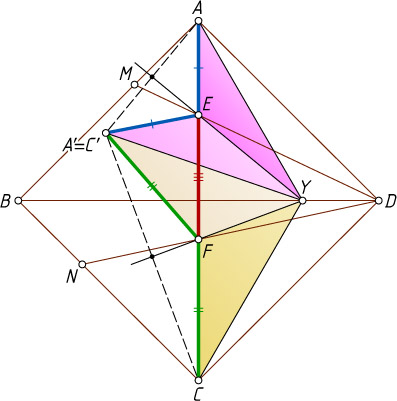
Пусть A'
— точка симметричная A
относительно прямой EY
, а C'
— точка, симметричная C
относительно прямой FY
. Поскольку
A'Y=AY=CY=C'Y,~\angle EYF=60^{\circ},
\angle EYA+\angle FYC=\angle AYC-\angle EYF=120^{\circ}-60^{\circ}=60^{\circ}=\angle EYF,
то точки A'
и C'
совпадают. При этом A'E=AE
, FA'=FC
. Таким образом, A'EF
— треугольник, составленный из отрезков AE
, EF
, FC
, причём
\angle EA'F=\angle EA'Y+\angle FA'Y=\angle EAY+\angle FCY=30^{\circ}+30^{\circ}=60^{\circ}.
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 288, с. 33



