11396. Две окружности касаются в точке P
. Прямая касается первой из них в точке A
и пересекает вторую в точках B
и C
. Докажите, что прямая PA
содержит биссектрису либо внутреннего, либо внешнего угла треугольника BPC
.
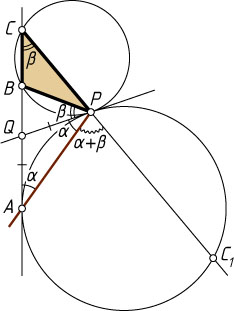
Решение. Пусть окружности касаются внешним образом (рис. 1), точка B
лежит между A
и C
, общая внутренняя касательная окружностей пересекает прямую AC
в точке Q
, а прямая CP
вторично пересекает первую окружность в точке C_{1}
. Обозначим
\angle APQ=\angle PAQ=\alpha,~\angle BCP=\angle BPQ=\beta
(см. задачу 89).
По теореме о внешнем угле треугольника
\angle APC_{1}=\angle PAC+\angle PCA=\alpha+\beta,
а так как
\angle APB=\angle APQ+\angle BPQ=\alpha+\beta,
то \angle APC_{1}=\angle APB
. Следовательно, луч PA
— биссектриса внешнего угла треугольника BPC
при вершине P
.
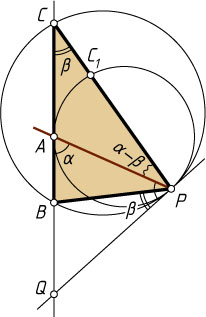
Пусть окружности касаются внутренним образом. В этом случае первая окружность лежит внутри второй (рис. 2). Тогда при тех же обозначениях
\angle APB=\alpha-\beta=\angle APC.
Следовательно, PA
— биссектриса внутреннего угла треугольника BPC
при вершине P
.
Источник: Люксембургские математические олимпиады. — 1980
Источник: Журнал «Crux Mathematicorum». — 1985, № 6, задача 4 (1981, с. 43), с. 171

