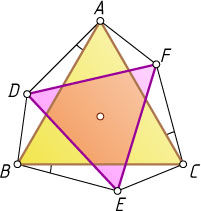
11787. Равносторонние треугольники ABC
и DEF
расположены так, как показано на рисунке, причём отмеченные углы равны. Докажите, что центры этих треугольников совпадают.
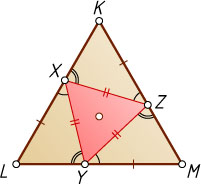
Решение. Лемма. Если вершины X
, Y
и Z
равностороннего треугольника XYZ
лежат на сторонах соответственно LM
, MK
и KL
равностороннего треугольника KLM
, то центры эти треугольников совпадают (рис. 1).
Доказательство. Треугольники KZY
, LXZ
и MYX
равны по стороне (ZY=XZ=YX
) и двум прилежащим к ней углам, поэтому KZ=LX=MY
. Значит, точки X
, Y
и Z
делят стороны треугольника KLM
в одном и том же отношении. Следовательно, центры треугольников KLM
и XYZ
совпадают (см. задачу 4512). Лемма доказана.
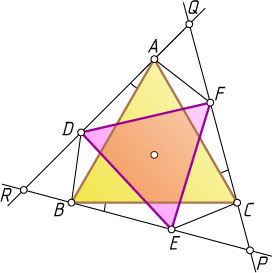
Вернёмся к нашей задаче (рис. 2). Пусть прямые BE
и CF
пересекаются в точке P
, прямые CF
и AD
— в точке Q
, а прямые AD
и BE
— в точке R
. Тогда по теореме о внешнем угле треугольника
\angle QPR=\angle QCB-\angle CBP=\angle QCB-\angle QCA=\angle ACB=60^{\circ}.
Аналогично для других углов треугольника PQR
. Значит, треугольник PQR
равносторонний, и по лемме его центр совпадает с центром равностороннего треугольника DEF
. В то же время, по той же лемме центр треугольника ABC
совпадает с центром PQR
. Отсюда следует утверждение задачи.
Источник: Журнал «Crux Mathematicorum». — 1983, № 6, задача 745 (1982, с. 136), с. 187


