11869. Докажите, что сумма квадратов расстояний от вершин квадрата, до произвольной точки описанной около него окружности, постоянна. Чему равна эта сумма, если сторона квадрата равна a
?
Ответ. 4a^{2}
.
Решение. Первый способ. Поместим начало координат в центр O
квадрата ABCD
(см. рис.), а оси Ox
и Oy
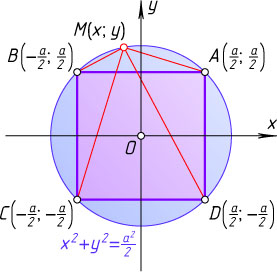
направим по лучам, параллельным соседним сторонам квадрата. Тогда уравнение окружности, описанной около квадрата, имеет вид x^{2}+y^{2}=\frac{a^{2}}{2}
(см. задачу 4202), а вершины квадрата имеют координаты A\left(\frac{a}{2};\frac{a}{2}\right)
, B\left(-\frac{a}{2};\frac{a}{2}\right)
, C\left(-\frac{a}{2};-\frac{a}{2}\right)
, D\left(\frac{a}{2};-\frac{a}{2}\right)
.
Пусть M(x;y)
— произвольная точка на окружности, описанной около квадрата. Тогда x^{2}+y^{2}=\frac{a^{2}}{2}
. Следовательно (см. задачу 4201),
MA^{2}+MB^{2}+MC^{2}+MD^{2}=
=\left(\left(x-\frac{a}{2}\right)^{2}+\left(y-\frac{a}{2}\right)^{2}\right)+\left(\left(x+\frac{a}{2}\right)^{2}+\left(y-\frac{a}{2}\right)^{2}\right)+
+\left(\left(x+\frac{a}{2}\right)^{2}+\left(y+\frac{a}{2}\right)^{2}\right)+\left(\left(x-\frac{a}{2}\right)^{2}+\left(y+\frac{a}{2}\right)^{2}\right)=
=4x^{2}+4y^{2}+8\cdot\frac{a^{2}}{4}=4(x^{2}+y^{2})+2a^{2}=4\cdot\frac{a^{2}}{2}+2a^{2}=4a^{2}.
Что и требовалось.
Второй способ.
MA^{2}+MB^{2}+MC^{2}+MD^{2}=\overrightarrow{MA}^{2}+\overrightarrow{MB}^{2}+\overrightarrow{MC}^{2}+\overrightarrow{MD}^{2}=
=(\overrightarrow{OA}-\overrightarrow{OM})^{2}+(\overrightarrow{OB}-\overrightarrow{OM})^{2}+(\overrightarrow{OC}-\overrightarrow{OM})^{2}+(\overrightarrow{OD}-\overrightarrow{OM})^{2}=
=4\overrightarrow{OA}^{2}-2\overrightarrow{OM}(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD})+4\overrightarrow{OM}^{2}=
=4OA^{2}+2\overrightarrow{OM}\cdot\overrightarrow{0}+4OM^{2}=4\cdot\frac{a^{2}}{2}+4\cdot\frac{a^{2}}{2}=4a^{2}.
Источник: Готман Э. Г. Задачи по планиметрии и методы их решения. — М.: Просвещение, 1996. — № 300, с. 83
