1195. Высота прямоугольного треугольника, опущенная на гипотенузу, равна 1, один из острых углов равен 15^{\circ}
. Найдите гипотенузу.
Ответ. 4.
Указание. Проведите медиану из вершины прямого угла.
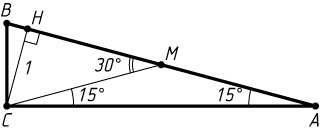
Решение. Пусть CH
— высота прямоугольного треугольника ABC
, проведённая из вершины прямого угла C
, \angle A=15^{\circ}
. Проведём медиану CM
. Тогда CM=AM=MB
(см. задачу 1109), \angle CMH
— внешний угол равнобедренного треугольника AMC
. Поэтому \angle CMH=30^{\circ}
. Из прямоугольного треугольника CMH
находим, что CM=2CH=2
. Следовательно, AB=2AM=2CM=4
.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — с. 8
