11953. Две прямые, пересекающие противоположные стороны четырёхугольника ABCD
, делят его на четыре четырёхугольника, в каждый из которых можно вписать окружность. Докажите, что отрезки прямых внутри четырёхугольника ABCD
равны. Докажите также, что в четырёхугольник ABCD
можно вписать окружность.
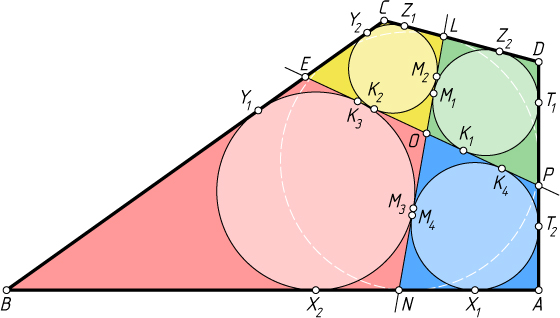
Решение. Пусть одна из прямых, пересекающихся в точке O
, пересекает стороны AB
и CD
четырёхугольника ABCD
в точках N
и L
соответственно (см. рисунок), вторая прямая пересекает стороны BC
и AD
в точках E
и P
соответственно; окружность, вписанная в четырёхугольник ANOP
, касается его сторон AN
, NO
, OP
и PA
в точках X_{1}
, M_{4}
, K_{4}
и T_{2}
соответственно; окружность, вписанная в четырёхугольник NBEO
, касается его сторон BE
, EO
, ON
и NB
в точках Y_{1}
, K_{3}
, M_{3}
и X_{2}
соответственно; окружность, вписанная в четырёхугольник CLOE
, касается его сторон CL
, LO
, OE
и EC
в точках Z_{1}
, M_{2}
, K_{2}
и Y_{2}
соответственно; окружность, вписанная в четырёхугольник DPOL
, касается его сторон DP
, PO
, OL
и LD
в точках T_{1}
, K_{1}
, M_{1}
и Z_{2}
соответственно.
Отрезок общей внутренней касательной двух окружностей, заключённый между двумя внешними их общими касательными, равен отрезку общей внешней касательной, заключённому между точками касания (см. задачу 4805в), значит,
PE=PO+OE=M_{1}M_{4}+M_{2}M_{3}=(M_{1}O+OM_{4})+(M_{2}O+OM_{3})=
=(K_{1}O+OK_{4})+(K_{2}O+OK_{3})=(K_{1}O+K_{2}O)+(OK_{4}+OK_{3})=
=K_{1}K_{2}+K_{3}K_{4}=LO+ON=LN.
Тогда (см. задачу 4805в)
X_{1}X_{2}+Z_{1}Z_{2}=ON+OL=LN=PE=PO+OE=T_{1}T_{2}+Y_{1}Y_{2},
а так как
AX_{1}=AT_{2},~BY_{1}=BX_{2},~CZ_{1}=CY_{2},~DT_{1}=DZ_{2},
то
AB+CD=BC+AD.
Следовательно, в четырёхугольник ABCD
можно вписать окружность.
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 967, с. 119
