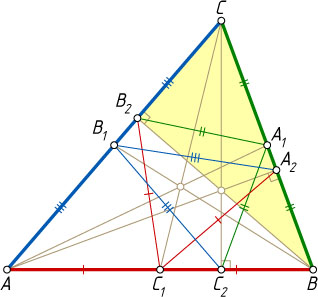
1196. В треугольнике ABC
проведены медианы AA_{1}
, BB_{1}
, CC_{1}
и высоты AA_{2}
, BB_{2}
, CC_{2}
. Докажите, что длина ломаной A_{1}B_{2}C_{1}A_{2}B_{1}C_{2}A_{1}
равна периметру треугольника ABC
.
Указание. Медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы.
Решение. Заметим, что A_{1}B_{2}
— медиана прямоугольного треугольника BB_{2}C
, проведённая к гипотенузе BC
, поэтому A_{1}B_{2}=\frac{1}{2}BC
(см. задачу 1109). Остальное аналогично.
