12055. Пусть M
— точка внутри параллелограмма ABCD
. Что больше: сумма расстояний от точки M
до вершин параллелограмма или его периметр?
Ответ. Периметр параллелограмма больше.
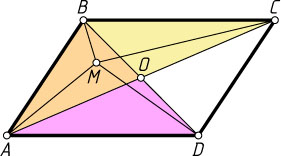
Решение. Первый способ. Пусть, для определённости, точка M
лежит внутри треугольника OAB
, где O
— точка пересечения диагоналей параллелограмма, т. е. внутри каждого из треугольников ABC
и BAD
(рис. 1). Тогда
AM+MC\leqslant AB+BC
(см. задачу 3502), причём равенство только при совпадении точек M
и B
, и
BM+MD\leqslant BA+AD,
причём равенство при совпадении M
и D
. Остаётся сложить эти неравенства.
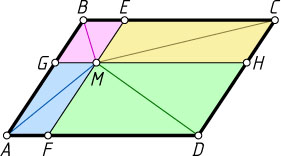
Второй способ. Пусть прямая, проведённая через точку M
параллельно AB
, пересекает стороны BC
и AD
в точках E
и F
соответственно, а прямая, проведённая через точку M
параллельно BC
, пересекает стороны AB
и CD
в точках G
и H
соответственно (рис. 2). Тогда по неравенству треугольника
MA\lt AG+GM=AG+AF,~MB=GB+GM=GB+BE,~
MC\lt CH+HM=CH+EC,~MD=HD+HM=DH+DF.
Сложив эти неравенства, получим
MA+MB+MC+MD\lt
\lt(AG+AF)+(GB+BE)+(CH+EC)+(HD+FD)=
=(AG+GB)+(BE+EC)+(CH+HD)+(AF+FD)=
=AB+BC+CD+AD.
Следовательно, периметр параллелограмма больше.