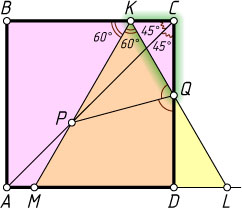
12086. Квадрат ABCD
и равносторонний треугольник MKL
расположены так, как это показано на рисунке (вершина K
равностороннего треугольника KLM
лежит на стороне BC
квадрата, вершина M
— на стороне AD
, вершина L
— на продолжении стороны AD
за точку D
, P
— точка пересечения отрезков AC
и KM
, Q
— точка пересечения отрезков CD
и KL
). Найдите угол PQD
.

Ответ. 75^{\circ}
Решение. Поскольку
\angle BKM=\angle LMK=60^{\circ}=\angle LKM,
луч KM
— биссектриса угла внешнего угла при вершине K
прямоугольного треугольника KCQ
, а так как CP
— биссектриса внутреннего угла при вершине C
этого треугольника, то QP
— биссектриса внешнего угла при вершине Q
(см. задачу 1192).
Следовательно,
\angle PQD=\frac{1}{2}\angle KQD=\frac{1}{2}(180^{\circ}-\angle CQK)=\frac{1}{2}(180^{\circ}-30^{\circ})=75^{\circ}.
Автор: Блинков Ю. А.
Источник: Олимпиада по геометрии им. И. Ф. Шарыгина. — 2015, XI, задача 2, 8-9 классы
Источник: Московская устная олимпиада по геометрии. — 2015, XIII, задача 2, 8-9 классы

