1210. С помощью циркуля и линейки постройте треугольник по трём медианам.
Указание. Сведите задачу к построению треугольника по двум сторонам и медиане, проведённой к третьей (см. задачу 1209).
Решение. Предположим, что задача решена. Пусть AA_{1}
, BB_{1}
и CC_{1}
— медианы построенного треугольника, M
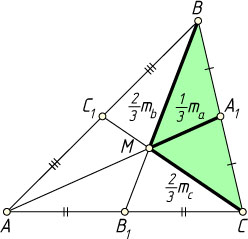
— точка их пересечения. Рассмотрим треугольник CMB
. Его можно построить по двум сторонам (CM=\frac{2}{3}CC_{1}
, BM=\frac{2}{3}BB_{1}
) и медиане, проведённой к третьей (MA_{1}=\frac{1}{3}AA_{1}
), см. задачу 1209.
Источник: Адамар Ж. Элементарная геометрия. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1948. — № 79(3), с. 94
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 8(1), с. 93
Источник: Зетель С. И. Новая геометрия треугольника. — М.: Учпедгиз, 1962. — с. 28
Источник: Пойа Д. Математическое открытие. — М.: Наука, 1970. — с. 34
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 8.13, с. 198
Источник: Голубев В. И., Ерганжиева Л. Н., Мосевич К. К. Построение треугольника. — М.: БИНОМ. Лаборатория Знаний, 2008. — № 163, с. 192
