12142. Точки A
, B
, C
, D
, E
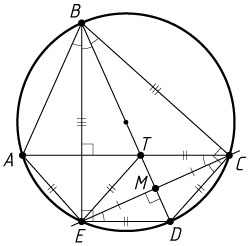
лежат на окружности в указанном порядке, причём AE=ED=CD
, а прямые AC
и BE
перпендикулярны. Отрезки AC
и BD
пересекаются в точке T
.
а) Докажите, что прямая EC
пересекает отрезок TD
в его середине.
б) Найдите площадь треугольника ABT
, если BD=6
, AE=\sqrt{6}
.
Ответ. \frac{8\sqrt{5}}{3}
.
Решение. а) Равные хорды AE
и CD
стягивают равные дуги, поэтому \angle ACE=\angle CED
. Значит, AC\parallel DE
. Тогда DE\perp BE
. Из точки E
, лежащей на окружности, хорда BD
видна под прямым углом, поэтому BD
— диаметр окружности, и \angle BCD=90^{\circ}
.
Поскольку \angle DBE=\angle DBC
, прямоугольные треугольники DBE
и DBC
равны по общей гипотенузе и острому углу, значит, DE=DC
и BE=BC
. Точки D
и B
равноудалены от концов хорды EC
, значит, DB
— серединный перпендикуляр к этой хорде. Следовательно, прямая BD
проходит через середину M
отрезка CE
.
Из равенства прямоугольных треугольников EMD
и CMT
по катету и противолежащему острому углу получаем, что CT=DE
, а так как CT\parallel DE
, то CDET
— параллелограмм (даже ромб). Следовательно, M
— середина TD
. Что и требовалось доказать.
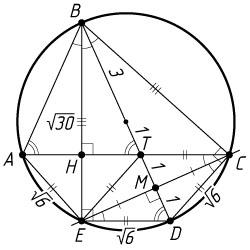
б) По теореме Пифагора
BE=\sqrt{BD^{2}-DE^{2}}=\sqrt{36-6}=\sqrt{30}.
Отрезок EM
— высота прямоугольного треугольника BED
, поэтому (см. задачу 1967)
EM=\frac{BE\cdot DE}{BD}=\frac{\sqrt{30}\cdot\sqrt{6}}{6}=\sqrt{5}.
Тогда
DM=\sqrt{DE^{2}-EM^{2}}=\sqrt{6-5}=1.
Пусть хорды BE
и AC
пересекаются в точке H
. Треугольник ABT
равнобедренный, так как его высота BH
является биссектрисой (вписанные углы ABE
и DBE
опираются на равные дуги). Значит,
AB=BT=BD-2DM=6-2=4.
Прямоугольные треугольники BHT
и BED
подобны с коэффициентом \frac{BT}{BD}=\frac{4}{6}=\frac{2}{3}
. Следовательно,
S_{\triangle ABT}=2S_{\triangle BHT}=2\cdot\left(\frac{2}{3}\right)^{2}\cdot S_{\triangle BED}=\frac{8}{9}\cdot\frac{1}{2}BE\cdot DE=\frac{8}{9}\cdot\frac{1}{2}\cdot\sqrt{30}\cdot\sqrt{6}=\frac{8\sqrt{5}}{3}.
Источник: ЕГЭ. — 2021, 7 июня, задача 16

