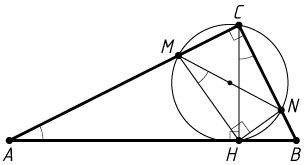
12316. Отрезок CH
— высота прямоугольного треугольника с прямым углом C
. На катетах AC
и BC
выбраны точки M
и N
, причём \angle MHN=90^{\circ}
.
а) Докажите, что треугольник MNH
подобен треугольнику ABC
.
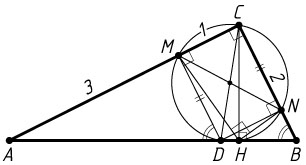
б) Найдите CN
, если BC=2
, AC=4
, CM=1
.
Ответ. \frac{3}{2}
.
Решение. а) В четырёхугольнике CMHN
углы NCM
и MHN
равны 90^{\circ}
. Следовательно, около этого четырёхугольника можно описать окружность (см. задачу 6). Значит,
\angle NMH=\angle NCH=90^{\circ}-\angle HBC=\angle BAC.
Таким образом, прямоугольные треугольники ABC
и MNH
подобны по двум углам.
б) Обозначим вторую точку пересечения окружности, описанной около четырёхугольника CMHN
, и отрезка AB
через D
. Тогда CD
— диаметр окружности, поскольку \angle CHD=90^{\circ}
(см. задачу 1689). Значит,
\angle CND=\angle CMD=\angle MCN=90^{\circ},
следовательно, четырёхугольник CNDM
— прямоугольник. Таким образом,
CN=DM=AM\tg\angle BAC=(AC-CM)\cdot\frac{BC}{AC}=(4-1)\cdot\frac{2}{4}=\frac{3}{2}.
Источник: ЕГЭ. — 2021

