12322. Окружность, вписанная в треугольник OMN
, касается сторон OM
, ON
и MN
в точках A
, B
и E
соответственно. Вневписанная окружность касается стороны MN
и продолжений сторон ON
и OM
в точках F
, C
и D
соответственно.
а) Докажите, что ME=NF
.
б) Найдите отношение площадей треугольников ABE
и CDF
, если радиус вписанной окружности равен 2, радиус вневписанной окружности равен 4.
Ответ. 1:2
.
Решение. а) См. задачу 4805б.
б) Пусть O_{1}
и O_{2}
— центры соответственно вписанной и вневписанной окружностей треугольника OMN
. Треугольники ABO_{1}
и CDO_{2}
подобны, поэтому
\frac{AB}{CD}=\frac{AO_{1}}{DO_{2}}=\frac{2}{4}=\frac{1}{2}.
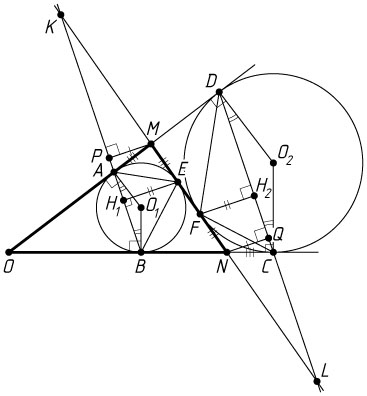
Рассмотрим равнобедренную трапецию ABCD
. Пусть прямая MN
пересекает прямые AB
и CD
в точках K
и L
соответственно, P
и H_{1}
— проекции точек соответственно M
и E
на прямую AB
, Q
и H_{2}
— проекции точек соответственно N
и F
на прямую CD
. Прямоугольные треугольники PAM
и QCN
равны по гипотенузе и острому углу, следовательно, PM=NQ
. Прямоугольные треугольники NQL
и MPK
равны по катету и противолежащему острому углу, значит,
KM=NL,~KE=KM+ME=FN+NL=FL.
Значит, прямоугольные треугольники EKH_{1}
и FLH_{2}
равны по гипотенузе и острому углу. Тогда EH_{1}=FH_{2}
. Следовательно,
\frac{S_{\triangle ABE}}{S_{\triangle CDF}}=\frac{\frac{1}{2}AB\cdot EH_{1}}{\frac{1}{2}CD\cdot FH_{2}}=\frac{AB}{CD}\cdot\frac{EH_{1}}{FH_{2}}=\frac{AB}{CD}=\frac{AO_{1}}{DO_{2}}=\frac{1}{2}.
Источник: Диагностические и тренировочные задачи ЕГЭ. — 2020
