12323. Диагонали равнобедренной трапеции ABCD
с основаниями AD
и BC
перпендикулярны. Окружность с диаметром AD
пересекает боковую сторону CD
в точке M
, а окружность с диаметром CD
пересекает основание AD
в точке N
. Отрезки AM
и CN
пересекаются в точке P
.
а) Докажите, что точка P
лежит на диагонали BD
трапеции ABCD
.
б) Найдите расстояние от точки P
до боковой стороны AB
, если BC=7
, AD=17
.
Ответ. \frac{119}{13}
.
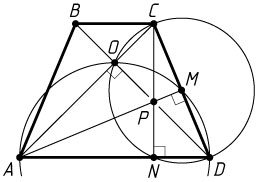
Решение. а) Точка M
лежит на окружности с диаметром AD
, поэтому AM\perp CD
, т. е. AM
— высота треугольника ACD
. Аналогично, CN
— высота треугольника ACD
. Пусть O
— точка пересечения диагоналей трапеции. По условию задачи DO\perp AC
, значит, DO
— третья высота треугольника ACD
. Высоты треугольника пересекаются в одной точке, следовательно, точка P
пересечения высот AM
и CN
лежит на прямой OD
, а значит, на диагонали BD
.
б) Отрезок CN
— высота равнобедренной трапеции, поэтому
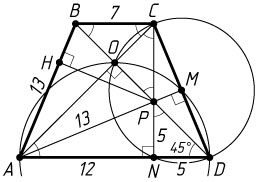
DN=\frac{AD-BC}{2}=\frac{17-7}{2}=5,AN=\frac{AD+BC}{2}=\frac{17+7}{2}=12
(см. задачу 1921). Диагонали равнобедренной трапеции образуют равные углы с основанием, а так как по условию диагонали перпендикулярны, то эти углы равны по 45^{\circ}
. Тогда
BP=CP\sqrt{2}=BC\sqrt{2}=7\sqrt{2},~AO=\frac{AD}{\sqrt{2}}=\frac{17}{\sqrt{2}},
CN=AN=12,~PN=DN=5.
По теореме Пифагора
AB=CD=\sqrt{CN^{2}+DN^{2}}=\sqrt{12^{2}+5^{2}}=13.
Прямоугольные треугольники ANP
и CND
равны по двум катетам, поэтому AP=CD=AB
. Расстояние от точки P
до боковой стороны AB
равно высоте PH
равнобедренного треугольника APB
, опущенной на его боковую сторону AB
, а так как AO
—тоже высота этого треугольника, то AB\cdot PH=BP\cdot AO
. Следовательно,
PH=\frac{BP\cdot AO}{AB}=\frac{7\sqrt{2}\cdot\frac{17}{\sqrt{2}}}{13}=\frac{119}{13}.
