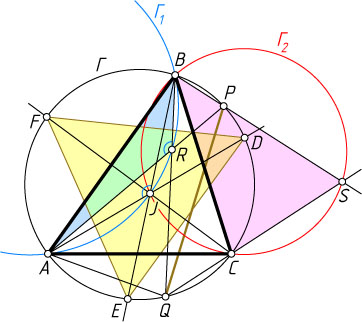
12351. Около треугольника ABC
описана окружность \Gamma
. Постройте точку J
треугольника ABC
, для которой лучи AJ
, BJ
и CJ
пересекают окружность \Gamma
в вершинах равностороннего треугольника.
Решение. Проведём хорду PQ
, которая видна из центра окружности под углом 120^{\circ}
. Рассмотрим случай, изображённый на рисунке. Приведённое ниже решение с небольшими изменениями годится для любого другого случая.
Пусть прямые AP
и BQ
пересекаются в точке R
, прямые CQ
и BP
— в точке S
, а описанные окружности \Gamma_{1}
и \Gamma_{2}
треугольников ABR
и BCS
соответственно — в точке J
, отличной от B
. Докажем, что J
— искомая точка.
Пусть лучи AJ
, BJ
и CJ
пересекают окружность \Gamma
в точках D
, E
и F
соответственно. Вписанные в окружность \Gamma_{1}
углы AJB
и ARB
опираются на одну и ту же дугу, поэтому \angle AJB=\angle ARB
, а так как хорды AD
и BE
окружности \Gamma
пересекаются в точке J
, то (см. задачу 26)
\angle AJB=\frac{1}{2}(\smile AFB+\smile DQE).
Аналогично,
\angle ARB=\frac{1}{2}(\smile AFB+\smile PDQ).
Значит, \smile DQE=\smile PDQ
, поэтому DE=PQ
, и тогда
\angle DFE=\angle PAQ=60^{\circ}.
Аналогично, \angle EDF=60^{\circ}
. Следовательно, треугольник DEF
равносторонний. Что и требовалось доказать.
Источник: Журнал «Crux Mathematicorum». — 1981, № 1, задача 504, с. 25
