1239. Средняя линия трапеции равна 4, углы при одном из оснований равны 40^{\circ}
и 50^{\circ}
. Найдите основания трапеции, если отрезок, соединяющий середины этих оснований, равен 1.
Ответ. 5 и 3.
Указание. Через середину меньшего основания проведите прямые, параллельные боковым сторонам трапеции.
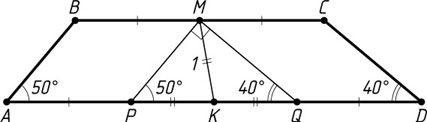
Решение. Пусть углы A
и D
при основании трапеции ABCD
равны 50^{\circ}
и 40^{\circ}
соответственно, M
и K
— середины оснований BC
и AD
. Через точку M
проведём прямую, параллельную AB
, до пересечения с AD
в точке P
и прямую, параллельную CD
до пересечения с AD
в точке Q
. Тогда
PK=AK-AP=AK-BM=KD-CM=KD-QD=KQ.
Поскольку
\angle PMQ=180^{\circ}-40^{\circ}-50^{\circ}=90^{\circ},
то MK
— медиана прямоугольного треугольника PMQ
, проведённая из вершины прямого угла PMQ
. Следовательно, PQ=2MK=2
(см. задачу 1109).
Поскольку
PQ=AD-AP-QD=AD-BM-MC=AD-BC,
то AD-BC=2
. Кроме того, по условию задачи AD+BC=8
. Из полученной системы уравнений находим, что AD=5
и BC=3
.
Источник: Вступительный экзамен на механико-математический факультет МГУ. — 1980, вариант 2, № 3
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — с. 9
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 1.16, с. 11
