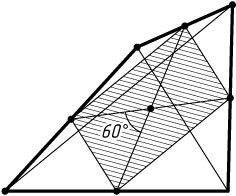
1240. В выпуклом четырёхугольнике отрезки, соединяющие середины противоположных сторон, равны соответственно a
и b
и пересекаются под углом 60^{\circ}
. Найдите диагонали четырёхугольника.
Ответ. \sqrt{a^{2}+b^{2}+ab}
, \sqrt{a^{2}+b^{2}-ab}
.
Указание. Середины сторон любого четырёхугольника являются вершинами параллелограмма (см. задачу 1204).
Решение. Середины сторон любого четырёхугольника являются вершинами параллелограмма (см. задачу 1204). В данном случае диагонали параллелограмма равны a
и b
, а угол между ними равен 60^{\circ}
.
Стороны параллелограмма найдём по теореме косинусов:
\frac{1}{2}\sqrt{a^{2}+b^{2}+ab},~\frac{1}{2}\sqrt{a^{2}+b^{2}-ab}.
Диагонали данного четырёхугольника в два раза больше соответствующих сторон параллелограмма.
Источник: Шарыгин И. Ф. Задачи по геометрии. Планиметрия. — 2-е изд. — М.: Наука, 1986. — № 123, с. 17
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 123, с. 15
