12404. Дан треугольник ABC
и произвольная точка P
, не лежащая на его описанной окружности. Точки M
, N
и O
— проекции точки P
на прямые BC
, AC
и AB
соответственно. Прямые AP
, BP
и CP
вторично пересекают описанную окружность треугольника ABC
в точках Q
, R
и S
соответственно. Докажите, что треугольники MNO
и QRS
подобны.
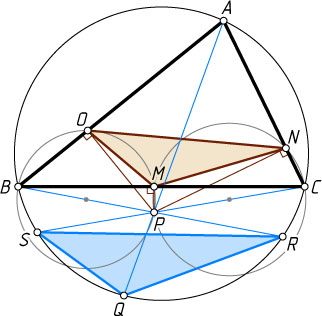
Решение. Рассмотрим случай, изображённый на рисунке. Приведённое ниже решение с небольшими изменениями годится для любого другого случая.
Четырёхугольники PMOB
и PMNC
вписанные, поэтому
\angle OMN=(180^{\circ}-\angle OMP)+(180^{\circ}-\angle PMN)=
=\angle RBA+\angle SCA=\frac{1}{2}(\smile AR+\smile SA)=
=\frac{1}{2}\smile SAR=\angle SQR.
Аналогично, \angle MNO=\angle QRS
. Следовательно, треугольники MNO
и QRS
подобны по двум углам. Что и требовалось доказать.
Примечание. Если точка P
лежит на описанной окружности треугольника ABC
, то точки M
, O
и N
лежат на одной прямой — прямой Симсона (см. задачу 83).
Источник: Журнал «Crux Mathematicorum». — 1980, № 4, задача 456 (1979, с. 167), с. 128
