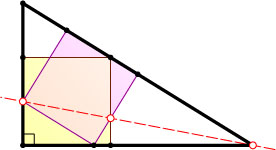
12410. В прямоугольный треугольник вписаны два квадрата, как показано на рисунке. Докажите, что три отмеченные точки лежат на одной прямой.
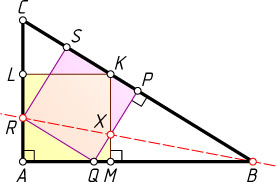
Решение. Пусть вершина K
квадрата KLAM
лежит на гипотенузе BC
прямоугольного треугольника ABC
, а вершины M
и L
— на катетах AB
и AC
соответственно; вершины Q
и R
квадрата QPSR
лежат на катетах AB
и AC
соответственно, а вершины P
и S
— на гипотенузе BC
; отрезки MK
и QP
пересекаются в точке X
. Требуется доказать, что точки B
, X
и R
лежат на одной прямой.
Из подобия прямоугольных треугольников BPQ
и BMK
получим
\frac{BP}{PS}=\frac{BP}{PQ}=\frac{BM}{MK}=\frac{BM}{MA}~\Rightarrow~\frac{BM}{BA}=\frac{BP}{PS}.
Значит, при гомотетии с центром B
, переводящей точку P
в S
, точка M
перейдёт в точку A
, прямая PQ
— в параллельную ей прямую SR
(см. задачу 5707), а прямая MK
— в параллельную ей прямую AC
. Тогда точка X
пересечения прямых PQ
и MK
перейдёт в точку R
пересечения прямых SR
и AC
. Следовательно, точки B
, X
и R
лежат на одной прямой.