1248. Медиана, проведённая к гипотенузе прямоугольного треугольника, равна m
и делит прямой угол в отношении 1:2
. Найдите стороны треугольника.
Ответ. 2m
, m
, m\sqrt{3}
.
Указание. Медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы.
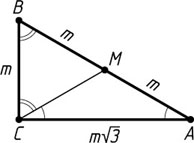
Решение. Пусть CM
— медиана прямоугольного треугольника ABC
, в котором \angle C=90^{\circ}
. Тогда CM=AM=BM=m
(см. задачу 1109), AB=2m
.
Если \angle BCM\gt\angle ACM
, то
\angle BCM=\frac{2}{3}\angle ACB=60^{\circ},~\angle ACM=30^{\circ}.
Поэтому \angle B=60^{\circ}
и треугольник BCM
— равносторонний. Следовательно,
BC=CM=m,~AC=BC\tg60^{\circ}=m\sqrt{3}.
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 10.021, с. 160
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 1.2, с. 10
