12515. Равносторонние треугольники ABC
и DKC
расположены так, как показано на рисунке (точка D
лежит на отрезке AB
, точки B
и K
по одну сторону от прямой AC
). Докажите, что BK\parallel AC
.
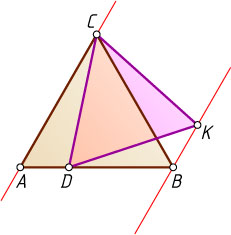
Решение. Первый способ. Треугольники DAC
и KBC
равны по двум сторонам (AC=BC
и DC=KC
как стороны равносторонних треугольников) и углу между ними
(\angle ACD=60^{\circ}-\angle DCB=\angle BCK).
Значит,
\angle CBK=\angle CAD=60^{\circ}=\angle BCA.
Следовательно, BK\parallel AC
.
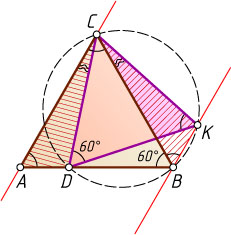
Второй способ. Из точек B
и K
, лежащих по одну сторону от прямой CD
, отрезок CD
виден под одним и тем же углом (60^{\circ}
), значит, точки C
, D
, B
и K
лежат на одной окружности (см. задачу 12). Вписанные в эту окружность углы CBK
и CDK
опираются на одну и ту же дугу, поэтому
\angle CBK=\angle CDK=60^{\circ}=\angle BCA.
Следовательно, BK\parallel AC
.
Источник: Всесибирская физико-математическая олимпиада. — 2019-2020, первый этап, задача 3, 8 класс

