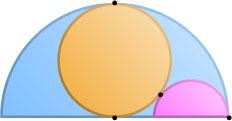
12530. Внутри полукруга радиуса 12 расположены круг радиуса 6, и маленький полукруг, касающиеся друг друга попарно, как показано на рисунке. Найдите радиус маленького полукруга.
Ответ. 4.
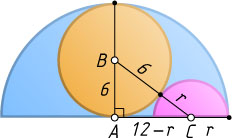
Решение. Пусть A
, B
и C
— центры большого полукруга, круга и маленького полукруга соответственно, а искомый радиус маленького полукруга равен r
. Поскольку диаметр круга равен радиусу полукруга, круг касается диаметра большого полукруга в точке A
.
Линия центров касающихся окружностей проходит через их точку касания (см. задачу 1758), поэтому
BC=6+r,~AC=12-r.
По теореме Пифагора
BC^{2}=AB^{2}+AC^{2},~\mbox{или}~(6+r)^{2}=36+(12-r)^{2},
откуда r=4
.
Источник: Всесибирская физико-математическая олимпиада. — 2014-2015, первый этап, задача 3, 9 класс

