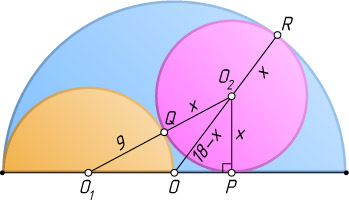
12534. В полукруге радиуса 18 на одной из половин диаметра построен полукруг радиуса 9, и вписан круг, касающийся большого полукруга изнутри, малого полукруга извне и второй половины диаметра. Найдите радиус этого круга.
Ответ. 8.
Решение. Обозначим через O
, O_{1}
, O_{2}
центры большого полукруга, малого полукруга и вписанного круга соответственно, а через P
, Q
, R
— точки касания вписанного круга с диаметром большого полукруга, с малым полукругом и большим полукругом соответственно. Тогда точки O_{1}
, Q
, O_{2}
лежат на одной прямой и точки O
, O_{2}
, R
лежат на одной прямой (см. задачу 1758).
Обозначим искомый радиус вписанного круга за x
. Тогда
O_{2}P=x,~O_{1}O_{2}=9+x,~OO_{2}=18-x.
Из прямоугольного треугольника OPO_{2}
получаем
OP=\sqrt{OO_{2}^{2}-O_{2}P^{2}}=\sqrt{(18-x)^{2}-x^{2}}=\sqrt{324-36x},
а из прямоугольного треугольника O_{1}O_{2}P
—
O_{1}P=\sqrt{O_{1}O_{2}^{2}-O_{2}P^{2}}=\sqrt{(9+x)^{2}-x^{2}}=\sqrt{81+18x}.
Тогда
O_{1}P=OP+OO_{1},~\mbox{или}~\sqrt{81+18x}=\sqrt{324-36x}+9.
После деления на 3 получаем уравнение
\sqrt{9+2x}=\sqrt{36-4x}+3,
из которого находим, что x=8
.
Источник: Всесибирская физико-математическая олимпиада. — 2014-2015, первый этап, задача 4, 11 класс
