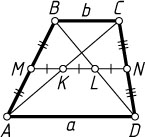
1255. Найдите отношение оснований трапеции, если известно, что её средняя линия делится диагоналями на три равные части.
Ответ. 1:2
.
Указание. Примените теорему о средней линии треугольника и задачу 1226.
Решение. Пусть AD=a
, BC=b
— основания трапеции ABCD
(a\gt b
), M
и N
— середины боковых сторон AB
и CD
соответственно, K
и L
— точки пересечения средней линии MN
с диагоналями AC
и BD
соответственно. Тогда точки K
и L
лежат на отрезке MN
(см. задачу 1226), и
MK=LN=\frac{1}{2}BC=\frac{b}{2}
как средние линии треугольников ABC
и DBC
.
По условию задачи KL=MK=LN=\frac{b}{2}
. Поэтому
MN=\frac{a+b}{2}=\frac{3b}{2}.
Отсюда находим, что a=2b
.