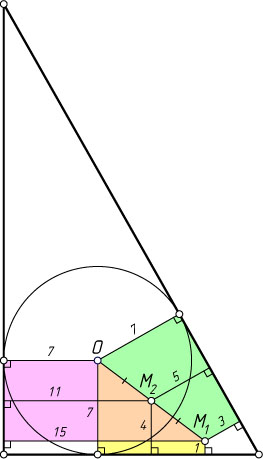
1260. Внутри треугольника имеются две точки. Расстояние от одной из них до сторон треугольника равны 1, 3 и 15, а от другой (в том же порядке) — 4, 5 и 11. Найдите радиус окружности, вписанной в данный треугольник.
Ответ. 7.
Указание. Пусть M_{1}
и M_{2}
— данные точки. На прямой M_{1}M_{2}
возьмите такую точку O
, что OM_{2}=M_{2}M_{1}
. Тогда O
— центр вписанной окружности данного треугольника.
Решение. Первый способ. Пусть M_{1}
и M_{2}
— данные точки; O
— такая точка, для которой M_{2}
есть середина OM_{1}
. По свойству средней линии трапеции расстояние от точки O
до сторон треугольника равны соответственно
2\cdot4-1=7,~2\cdot5-3=7,~2\cdot11-15=7.
Поскольку отрезок OM_{1}
не может пересекать ни одной из сторон треугольника, то O
— центр вписанной в данный треугольник окружности, а её радиус равен 7.
Второй способ. Пусть точки M
и N
расположены внутри треугольника ABC
со сторонами BC=a
, AC=b
и AB=c
, причём точка M
удалена от сторон BC
, AC
и AB
на расстояния 1, 3 и 15, а точка N
— на расстояния 4, 5 и 11 соответственно. Тогда, если S
— площадь треугольника ABC
, то
\syst{a+3b+15c=2S\\4a+5b+11c=2S.\\}
Умножим второе равенство на 2 и вычтем из него первое. Учитывая, что
2S=(a+b+c)r,
где r
— радиус вписанной окружности треугольника ABC
(см. задачу 452), получим, что
7a+7b+7c=2S=r(a+b+c).
Отсюда находим, что r=7
.
Источник: Журнал «Математика в школе». — 1991, № 2, с. 62, № 3548
Источник: Мерзляк А. Г., Поляков В. М. Геометрия. 8 класс. Углублённый уровень. — М.: Вентана-Граф, 2019. — № 25.57, с. 185
