1263. Медиана прямоугольного треугольника, проведённая к гипотенузе, разбивает его на два треугольника с периметрами m
и n
. Найдите стороны треугольника.
Ответ. \sqrt{2mn}-m
, \sqrt{2mn}-n
, n+m-\sqrt{2mn}
.
Указание. Составьте систему уравнений относительно катетов треугольника, учитывая, что указанная медиана равна половине гипотенузы.
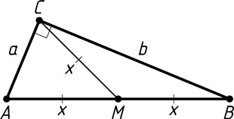
Решение. Пусть a
и b
— катеты треугольника, x
— медиана, проведённая к гипотенузе. Тогда гипотенуза равна 2x
(см. задачу 1109).
Предположим, что a\lt b
. Тогда по условию задачи 2x+b=m
и 2x+a=n
. Отсюда следует, что b=a+m-n
. Поскольку 2x=\sqrt{a^{2}+b^{2}}
, то
\syst{b=a+m-n\\2\sqrt{a^{2}+b^{2}}+a+b=m+n.\\}
Из этой системы находим, что
a=\sqrt{2mn}-m,~b=\sqrt{2mn}-n,~2x=n+m-\sqrt{2mn}.
Источник: Вступительный экзамен в МАТИ. — № 5, 1989
Источник: Журнал «Квант». — 1990, № 5, с. 68
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 1.10, с. 10
