12756. Геометрический смысл классических неравенств. Окружности с центрами O_{1}
и O_{2}
различных радиусов соответственно r
и R
(r\lt R
) касаются внешним образом. К ним проведены две общие внешние касательные. Их точки касания с первой окружностью — A
и D
, со второй — B
и C
соответственно. Радиусы O_{1}E
и O_{2}F
этих окружностей (точки E
и F
лежат по одну сторону от прямой O_{1}O_{2}
) перпендикулярны прямой O_{1}O_{2}
. 1) Найдите: а) O_{1}O_{2}
, б) AB
, в) расстояние между параллельными прямыми AD
и BC
, г) EF
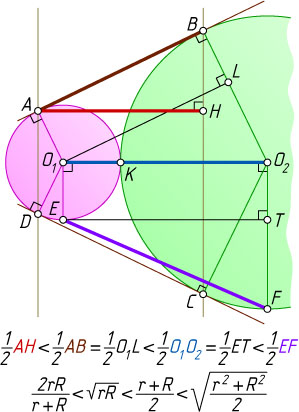
.
2) Расположив найденные величины по возрастанию, проиллюстрируйте неравенство о средних величинах двух положительных чисел r
и R
.
Ответ. 1) а) O_{1}O_{2}=r+R
, б) AB=2\sqrt{rR}
, в) d=\frac{4rR}{r+R}
, г) EF=\sqrt{2(r^{2}+R^{2})}
.
2) \frac{2rR}{r+R}\leqslant\sqrt{rR}\leqslant\frac{r+R}{2}\leqslant\sqrt{\frac{r^{2}+R^{2}}{2}}
.
Решение. 1) а) Линия центров касающихся окружностей проходит через точку их касания, а так как окружности касаются внешним образом, то точка касания K
лежит на отрезке O_{1}O_{2}
. Следовательно,
O_{1}O_{2}=O_{1}K+KO_{2}=r+R.
б) См. задачу 365.
в) См. задачу 4818.
г) Для определённости будем считать, что r\lt R
. Пусть T
— проекция точки E
на прямую O_{2}F
. Тогда O_{1}ETO_{2}
— прямоугольник, поэтому
ET=O_{1}O_{2}=r+R,~FT=O_{2}F-O_{2}T=O_{2}F-O_{1}E=R-r.
Следовательно,
EF=\sqrt{ET^{2}+FT^{2}}=\sqrt{(r+R)^{2}+(R-r)^{2}}=\sqrt{2(r^{2}+R^{2})}.
2) Пусть L
— проекция точки O_{1}
на прямую O_{2}B
. Тогда O_{1}ABL
— прямоугольник, поэтому O_{1}L=AB
. Отрезок O_{1}L
— катет прямоугольного треугольника O_{1}LO_{2}
с гипотенузой O_{1}O_{2}
, значит,
2\sqrt{rR}=AB=O_{1}L\lt O_{1}O_{2}=r+R.
Следовательно, r+R\gt2\sqrt{rR}
.
Пусть H
— проекция точки A
на прямую BC
. Отрезок AH
— катет прямоугольного треугольника AHB
с гипотенузой AB
, поэтому
\frac{4rR}{r+R}=AH\lt AB=2\sqrt{rR}.
Следовательно, 2\sqrt{rR}\gt\frac{4rR}{r+R}
.
Отрезок ET
— катет прямоугольного треугольника ETF
с гипотенузой EF
, поэтому
r+R=O_{1}O_{2}=ET\lt EF=\sqrt{2(r^{2}+R^{2})}.
Следовательно, r+R\lt\sqrt{2(r^{2}+R^{2})}
.
Таким образом,
\frac{4rR}{r+R}\lt2\sqrt{rR}\lt r+R\lt\sqrt{2(r^{2}+R^{2})},
или
\frac{2rR}{r+R}\lt\sqrt{rR}\lt\frac{r+R}{2}\lt\sqrt{\frac{r^{2}+R^{2}}{2}}.
Примечание. 1. Число \frac{a+b}{2}
называется средним арифметическим чисел a
и b
,
\sqrt{ab}
— средним геометрическим чисел a
и b
,
\frac{2ab}{a+b}
— средним гармоническим чисел a
и b
,
\sqrt{\frac{a^{2}+b^{2}}{2}}
— средним квадратичным (средним квадратическим) чисел a
и b
.
Для любых двух неотрицательных чисел a
и b
верно неравенство
\frac{2ab}{a+b}\leqslant\sqrt{ab}\leqslant\frac{a+b}{2}\leqslant\sqrt{\frac{a^{2}+b^{2}}{2}},
причём равенство достигается тогда и только тогда, когда a=b
(в нашем случае r=R
).
2. Число \frac{a_{1}+a_{2}+\dots+a_{n}}{n}
называется средним арифметическим чисел a_{1}
, a_{2}
, …, a_{n}
;
\sqrt[{n}]{{a_{1}a_{2}\dots a_{n}}}
— средним геометрическим чисел a_{1}
, a_{2}
, …, a_{n}
;
\frac{n}{\frac{1}{a_{1}}+\frac{1}{a_{2}}+\dots+\frac{1}{a_{n}}}
— средним гармоническим чисел a_{1}
, a_{2}
, …, a_{n}
;
\sqrt{\frac{a_{1}^{2}+a_{2}^{2}+\dots+a_{n}^{2}}{n}}
— средним квадратичным (средним квадратическим) чисел a_{1}
, a_{2}
, …, a_{n}
.
Для любых положительных чисел a_{1}
, a_{2}
, …, a_{n}
верно неравенство
\frac{n}{\frac{1}{a_{1}}+\frac{1}{a_{2}}+\dots+\frac{1}{a_{n}}}\leqslant\sqrt[{n}]{{a_{1}a_{2}\dots a_{n}}}\leqslant\frac{a_{1}+a_{2}+\dots+a_{n}}{n}\leqslant\sqrt{\frac{a_{1}^{2}+a_{2}^{2}+\dots+a_{n}^{2}}{n}},
причём равенство достигается тогда и только тогда, когда a_{1}=a_{2}=\dots=a_{n}
.
3. См. также статью З.А.Скопеца «Сравнение различных средних двух положительных чисел», Квант, 1971, N2, с.20-33.
4. См. также статью А.Гольдмана и Л.Звавича «Числовые средние и геометрия», Квант, 1990, N9, с.62-65.
5. См. также статью Л.Шибасова «Соотношения между средними величинами», Квант, 2004, N4, с.42-46.
