1276. Радиусы OA
и OB
высекают на окружности с центром O
дугу величиной 60^{\circ}
. На этой дуге взята точка M
. Докажите, что прямая, проходящая через середины отрезков MA
и OB
, перпендикулярна прямой, проходящей через середины отрезков MB
и OA
.
Указание. Указанные отрезки являются диагоналями ромба (см. задачу 1204).
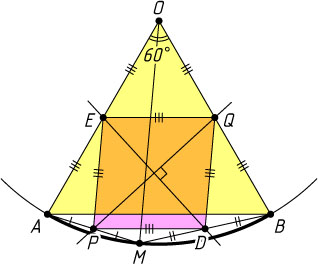
Решение. Пусть P
, D
, Q
, E
— середины сторон соответственно AM
, MB
, BO
, AO
четырёхугольника AMBO
. Тогда PDQE
— параллелограмм (см. задачу 1204). Поскольку треугольник AOB
равносторонний,
PD=\frac{1}{2}AB=\frac{1}{2}AO=\frac{1}{2}OM=DQ.
Следовательно, PDQE
— ромб. Поэтому PQ\perp DE
.
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 1.11, с. 11
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 1.11, с. 13
