12787. Дан четырёхугольник ABCD
и окружность, касающаяся сторон AD
, DC
и CB
в точках K
, L
и M
соответственно. Прямая, проходящая через точку L
параллельно AD
, пересекает отрезок KM
в точке N
; P
— точка пересечения LN
и KC
. Докажите, что PL=PN
.
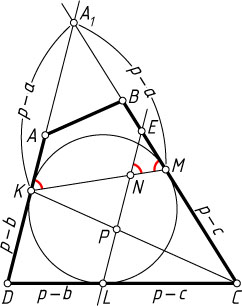
Решение. Рассмотрим случай, изображённый на рисунке 1. Пусть лучи DA
и CB
пересекаются в точке A_{1}
. Тогда получим треугольник A_{1}DC
и вписанную в него окружность, касающуюся сторон A_{1}D=c
, DC=a
и CA_{1}=b
в точках K
, L
и M
соответственно. Обозначим \frac{a+b+c}{2}=p
— полупериметр треугольника.
Пусть прямая LN
пересекает сторону CA_{1}
в точке E
. Поскольку
\angle EMN=\angle A_{1}MN=\angle A_{1}KM=\angle ENM,
треугольник EMN
равнобедренный, а так как треугольник CEL
подобен треугольнику CA_{1}D
с коэффициентом \frac{CL}{CD}
, и CE=p-c
(см. задачу 68), то
EN=EM=CE-CM=CA_{1}\cdot\frac{CL}{CD}-CM=
=b\cdot\frac{p-c}{a}-(p-c)=\frac{(p-c)(b-a)}{a}.
Тогда
LN=LE-EN=A_{1}D\cdot\frac{CL}{CD}-EN=c\cdot\frac{p-c}{a}-\frac{(p-c)(b-a)}{a}=
=\frac{p-c}{a}(c-b+a)=\frac{2(p-c)(p-b)}{a}=
=2\cdot\frac{p-c}{a}\cdot(p-b)=2\cdot\frac{CL}{CD}\cdot DK=2LP.
Следовательно, LP=PN
. Что и требовалось доказать.
Аналогично для случая, когда A_{1}
— точка пересечения лучей AD
и BC
.
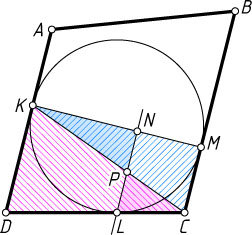
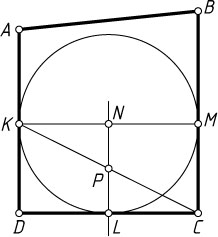
Если же AD\parallel CB
, то DKMC
— трапеция (рис. 2) или прямоугольник (рис. 3). В первом из этих случаев треугольник LCP
подобен треугольнику DCK
, а треугольник PKN
— треугольнику CKM
, поэтому
PL=DK\cdot\frac{CL}{CD}=DL\cdot\frac{CM}{CD}=CM\cdot\frac{DL}{CD}=CM\cdot\frac{KN}{KM}=PN.
Для второго случая утверждение очевидно.
Источник: Турецкие математические олимпиады. — 1996, задача 4
Источник: Журнал «Crux Mathematicorum». — 2002, № 8, задача 4, с. 502


