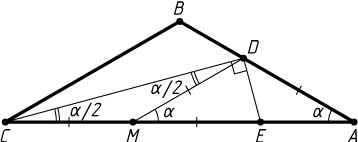
1280. В равнобедренном треугольнике ABC
с основанием AC
проведена биссектриса CD
. Прямая, проходящая через точку D
перпендикулярно DC
, пересекает AC
в точке E
. Докажите, что EC=2AD
.
Указание. Соедините точку D
с серединой отрезка CE
(или через точку D
проведите прямую, параллельную AC
).
Решение. Первый способ. Пусть DM
— медиана прямоугольного треугольника CDE
. Тогда DM=\frac{1}{2}CE
(см. задачу 1109). С другой стороны,
\angle DME=2\angle DCM=\angle BCA=\angle BAC.
Поэтому треугольник MDA
— равнобедренный. Следовательно, AD=DM=\frac{1}{2}EC
.
Второй способ. Пусть F
— точка пересечения прямых BC
и DE
, а L
— точка пересечения прямой, проведённой через точку D
параллельно AC
, со стороной BC
.
Треугольник CLD
равнобедренный (CL=LD
), так как
\angle CDL=\angle DCA=\angle DCL,
Значит, AD=CL=DL
.
Треугольник ECF
также равнобедренный (CF=CE
), так как его биссектриса CD
является высотой. Значит, D
— середина EF
, а DL
— средняя линия треугольника ECF
. Следовательно,
CE=2DL=2CL=2AD.
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 5.18, с. 106
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 5.21, с. 104
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 858, с. 105
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — с. 9
