12817. В треугольнике ABC
с неравными сторонами AB
и AC
проведены биссектриса AD
и медиана AM
. Докажите, что прямая, проходящая через центры описанных окружностей треугольников ABC
и ADM
параллельна AD
.
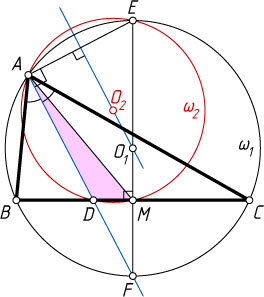
Решение. Без ограничения общности считаем, что AC\gt AB
(см. рис.). Пусть \omega_{1}
и \omega_{2}
— описанные окружности треугольников ABC
и ADM
соответственно, O_{1}
и O_{2}
— их центры, F
— точка пересечения луча AD
с окружностью \omega_{1}
.
Точка F
— середина дуги BC
, не содержащей точки A
(см. задачу 430), поэтому диаметр FE
окружности \omega_{1}
лежит на серединном перпендикуляре к отрезку BC
, а значит, проходит через точку M
.
Поскольку
\angle EAD=\angle EAF=90^{\circ}=\angle EMD,
точка E
лежит на окружности \omega_{2}
. Линия центров пересекающихся окружностей перпендикулярна их общей хорде, поэтому O_{1}O_{2}\perp AE
. Прямые AD
и O_{1}O_{2}
перпендикулярны одной и той же прямой AE
, следовательно, они параллельны. Что и требовалось доказать.
Источник: Журнал «Crux Mathematicorum». — 2023, № 1, задача OC589, с. 30
Источник: Польские математические олимпиады. —
