13090. Две равные касающиеся окружности единичного радиуса расположены внутри прямоугольника, причём каждая сторона прямоугольника касается хотя бы одной окружности (см. рис.). Найдите наибольшую и наименьшую площадь прямоугольника.
Ответ. 6+4\sqrt{2}
и 8.
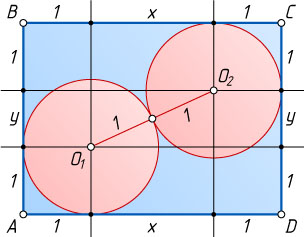
Решение. Через центры O_{1}
и O_{2}
проведём прямые, параллельные сторонам AB
и CD
прямоугольника ABCD
. Пусть расстояние между прямыми, параллельными AB
, равно x
, расстояние между прямыми, параллельными BC
, равно y
, а площадь прямоугольника равна S
. Тогда
S=(2+x)(2+y).
Прямоугольник разбит на девять частей: четыре квадрата со стороной 1, два прямоугольника со сторонами 1 и x
, два прямоугольника со сторонами 1 и y
и прямоугольник со сторонами x
и y
. При этом
x^{2}+y^{2}=O_{1}O_{2}^{2}=4.
Значит,
S=4+2x+2y+xy=4+2(x+y)+xy,
а так как (см. задачу 3399)
\frac{x+y}{2}\leqslant\sqrt{\frac{x^{2}+y^{2}}{2}}~\Rightarrow~x+y\leqslant\sqrt{2(x^{2}+y^{2})}~\mbox{и}~xy\leqslant\frac{x^{2}+y^{2}}{2},
то
S=4+2(x+y)+xy\leqslant4+2\sqrt{2(x^{2}+y^{2})}+\frac{x^{2}+y^{2}}{2}=
=4+2\sqrt{2\cdot4}+2=6+4\sqrt{2},
причём равенство достигается тогда и только тогда, когда x=y=\sqrt{2}
. Следовательно, наибольшее значение S
равно 6+4\sqrt{2}
.
В то же время,
S=(2+x)(2+y)=4+xy+2(x+y)=2+(2+xy)+2(x+y)=
=2+\left(\frac{x^{2}+y^{2}}{2}+xy\right)+2(x+y)=2+\frac{1}{2}(x+y)^{2}+2(x+y),
а так как
xy\geqslant0~\Rightarrow~x+y\geqslant\sqrt{x^{2}+y^{2}}=2,
то
S=2+\frac{1}{2}(x+y)^{2}+2(x+y)\geqslant2+\frac{1}{2}\cdot4+2\cdot2=8,
причём равенство достигается тогда и только тогда, когда x=2
, y=0
или x=0
, y=2
. Следовательно, наименьшее значение S
равно 8.
Источник: Журнал «Crux Mathematicorum». — 2021, № 8, задача OC521, с. 379
Источник: Математические олимпиады Чехии и Словакии. — 2018

