1314. С помощью циркуля и линейки постройте треугольник по двум углам и медиане, проведённой из вершины третьего угла.
Указание. На продолжении медианы отложите отрезок, равный медиане.
Решение. Пусть в треугольнике ABC
известны углы \angle B=\beta
и \angle C=\gamma
и медиана AD=m_{a}
, проведённая к стороне BC
. На продолжении отрезка AD
за точку D
возьмём точку A_{1}
так, что DA_{1}=AD
. В треугольнике AA_{1}B
известна сторона AA_{1}=2m_{a}
и углы \angle ABD=\beta
и \angle A_{1}BD=\angle ACB=\gamma
.
Из точки B
отрезок AD
виден под углом \beta
, а отрезок A_{1}D
— под углом \gamma
. Тогда вершина B
есть пересечение двух дуг, построенных на AD
и DA_{1}
, вмещающих углы \beta
и \gamma
соответственно и расположенных по одну сторону от прямой AA_{1}
Отсюда вытекает следующее построение.
Строим середину D
произвольного отрезка AA_{1}=2m_{a}
. На отрезке AD
как на хорде построим дугу окружности так, чтобы из каждой точки этой дуги отрезок AD
был виден под данным углом \beta
(см. задачу 2889). По ту же сторону от прямой AA_{1}
строим на отрезке A_{1}D
как на хорде дугу окружности так, чтобы из каждой точки этой дуги отрезок A_{1}D
был виден под данным углом \gamma
. Пусть B
— точка пересечения этих дуг, отличная от D
. На продолжении медианы BA_{1}
треугольника ABA_{1}
отложим отрезок A_{1}C
, равный BA_{1}
. Тогда треугольник ABC
— искомый.
Действительно, AD=\frac{1}{2}AA_{1}=m_{a}
— данная медиана,
\angle ABC=\angle ABD=\beta,~\angle ACB=\angle A_{1}BC=\angle A_{1}BD=\gamma
— данные углы.
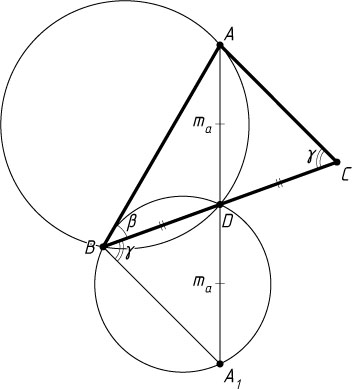
Источник: Шарыгин И. Ф. Геометрия — 8. Теория и задачи: Экспериментальное учебное пособие для 8 кл. — М.: РОСТ, МИРОС, 1996. — № 5.3.4, с. 33
Источник: Голубев В. И., Ерганжиева Л. Н., Мосевич К. К. Построение треугольника. — М.: БИНОМ. Лаборатория Знаний, 2008. — № 80, с. 114
