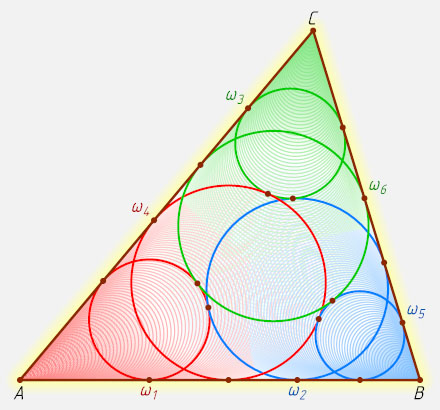
13154. Теорема о шести окружностях. Дан треугольник ABC
. Внутри него расположены шесть окружностей: окружность \omega_{1}
вписана в угол A
; окружность \omega_{2}
вписана в угол B
и внешним образом касается окружности \omega_{1}
; окружность \omega_{3}
вписана в угол C
и внешним образом касается окружности \omega_{2}
; окружность \omega_{4}
вписана в угол A
и внешним образом касается окружности \omega_{3}
; окружность \omega_{5}
вписана в угол B
и внешним образом касается окружности \omega_{4}
; окружность \omega_{6}
вписана в угол C
и внешним образом касается окружности \omega_{5}
. Докажите, что окружности \omega_{6}
и \omega_{1}
касаются.
Решение. Впишем в угол A
окружность \omega_{7}
, внешним образом касающуюся окружности \omega_{6}
. Обозначим AB=c
, BC=a
, CA=b
, \angle A=\alpha
, \angle B=\beta
, \angle C=\gamma
, p=\frac{a+b+c}{2}
, S
— площадь треугольника ABC
, а радиусы окружностей \omega_{1}
, …, \omega_{7}
— через r_{1}
, …, r_{7}
. Требуется доказать, что r_{1}=r_{7}
.
Спроецировав центры окружностей \omega_{1}
и \omega_{2}
на отрезок AB
, получаем равенство (см. задачу 365)
r_{1}\ctg\frac{\alpha}{2}+2\sqrt{r_{1}r_{2}}+r_{2}\ctg\frac{\beta}{2}=c.
Аналогично,
r_{2}\ctg\frac{\beta}{2}+2\sqrt{r_{2}r_{3}}+r_{3}\ctg\frac{\gamma}{2}=a,~r_{3}\ctg\frac{\gamma}{2}+2\sqrt{r_{3}r_{4}}+r_{4}\ctg\frac{\alpha}{2}=b,
r_{4}\ctg\frac{\alpha}{2}+2\sqrt{r_{4}r_{5}}+r_{5}\ctg\frac{\beta}{2}=c,~r_{5}\ctg\frac{\beta}{2}+2\sqrt{r_{5}r_{6}}+r_{6}\ctg\frac{\gamma}{2}=a,
r_{6}\ctg\frac{\gamma}{2}+2\sqrt{r_{6}r_{7}}+r_{7}\ctg\frac{\alpha}{2}=b.
Введём новые обозначения:
\rho_{1}^2=r_{1}\ctg\frac{\alpha}{2},~\rho_{2}^2=r_{2}\ctg\frac{\beta}{2},~\rho_{3}^2=r_{3}\ctg\frac{\gamma}{2},
\rho_{4}^2=r_{4}\ctg\frac{\alpha}{2},~\rho_{5}^2=r_{5}\ctg\frac{\beta}{2},~\rho_{6}^2=r_{6}\ctg\frac{\gamma}{2},~\rho_{7}^2=r_{7}\ctg\frac{\alpha}{2}.
Тогда ранее полученные равенства приобретают вид
\rho_{1}^2+\rho_{2}^2+2\rho_{1}\rho_{2}\sqrt{\tg\frac{\alpha}{2}\tg\frac{\beta}{2}}=c,~\rho_{4}^2+\rho_{5}^2+2\rho_{4}\rho_{5}\sqrt{\tg\frac{\alpha}{2}\tg\frac{\beta}{2}}=c,
\rho_{2}^2+\rho_{3}^2+2\rho_{2}\rho_{3}\sqrt{\tg\frac{\beta}{2}\tg\frac{\gamma}{2}}=a,~\rho_{5}^2+\rho_{6}^2+2\rho_{5}\rho_{6}\sqrt{\tg\frac{\beta}{2}\tg\frac{\gamma}{2}}=a,
\rho_{3}^2+\rho_{4}^2+2\rho_{3}\rho_{4}\sqrt{\tg\frac{\gamma}{2}\tg\frac{\alpha}{2}}=b,~\rho_{6}^2+\rho_{7}^2+2\rho_{6}\rho_{7}\sqrt{\tg\frac{\gamma}{2}\tg\frac{\alpha}{2}}=b.
Преобразуем подкоренные выражения:
\tg\frac{\alpha}{2}\tg\frac{\beta}{2}=\frac{S}{p(p-a)}\cdot\frac{S}{p(p-b)}=\frac{p(p-a)(p-b)(p-c)}{p^2(p-a)(p-b)}=1-\frac{c}{p}
(см. задачу 4884); и аналогично
\tg\frac{\beta}{2}\tg\frac{\gamma}{2}=1-\frac{a}{p},~\tg\frac{\gamma}{2}\tg\frac{\alpha}{2}=1-\frac{b}{p}.
Очевидно, существуют такие углы \varphi
, \chi
, \psi
из интервала (90^{\circ};180^{\circ})
, что
\cos\varphi=-\sqrt{1-\frac{c}{p}},~\sin\varphi=\sqrt{\frac{c}{p}},
\cos\chi=-\sqrt{1-\frac{a}{p}},~\sin\chi=\sqrt{\frac{a}{p}},
\cos\psi=-\sqrt{1-\frac{b}{p}},~\sin\psi=\sqrt{\frac{b}{p}}.
Таким образом, соотношения для \rho_{1}
, …, \rho_{7}
становятся теоремами косинусов
\rho_{1}^2+\rho_{2}^2-2\rho_{1}\rho_{2}\cos\varphi=(\sqrt{c})^2,~\rho_{4}^2+\rho_{5}^2-2\rho_{4}\rho_{5}\cos\varphi=(\sqrt{c})^2,
\rho_{2}^2+\rho_{3}^2-2\rho_{2}\rho_{3}\cos\chi=(\sqrt{a})^2,~\rho_{5}^2+\rho_{6}^2-2\rho_{5}\rho_{6}\cos\chi=(\sqrt{a})^2,
\rho_{3}^2+\rho_{4}^2-2\rho_{3}\rho_{4}\cos\psi=(\sqrt{b})^2,~\rho_{6}^2+\rho_{7}^2-2\rho_{6}\rho_{7}\cos\psi=(\sqrt{b})^2
для треугольников со сторонами \rho_{1}
, \rho_{2}
, \sqrt{c}
; \rho_{2}
, \rho_{3}
, \sqrt{a}
; \rho_{3}
, \rho_{4}
, \sqrt{b}
; \rho_{4}
, \rho_{5}
, \sqrt{c}
; \rho_{5}
, \rho_{6}
, \sqrt{a}
; \rho_{6}
, \rho_{7}
, \sqrt{b}
. Причём у этих шести треугольников один и тот же диаметр описанной окружности, равный \frac{\sqrt{c}}{\sin\varphi}=\frac{\sqrt{a}}{\sin\chi}=\frac{\sqrt{b}}{\sin\psi}=\sqrt{p}
.
Значит, можно построить ломаную X_{0}X_{1}X_{2}X_{3}X_{4}X_{5}X_{6}X_{7}
, вписанную в окружность с центром O
диаметра \sqrt{p}
, у которой
X_{0}X_{1}=\rho_{1},~X_{1}X_{2}=\rho_{2},~X_{2}X_{3}=\rho_{3},~X_{3}X_{4}=\rho_{4},~X_{4}X_{5}=\rho_{5},~X_{5}X_{6}=\rho_{6},~X_{6}X_{7}=\rho_{7};
\angle X_{0}X_{1}X_{2}=\angle X_{3}X_{4}X_{5}=\varphi,~\angle X_{1}X_{2}X_{3}=\angle X_{4}X_{5}X_{6}=\chi,~\angle X_{2}X_{3}X_{4}=\angle X_{5}X_{6}X_{7}=\psi;
X_{0}X_{2}=X_{3}X_{5}=\sqrt{c},~X_{1}X_{3}=X_{4}X_{6}=\sqrt{a},~X_{2}X_{4}=X_{5}X_{7}=\sqrt{b}.
Заметим, что точка O
лежит вне треугольников X_{0}X_{1}X_{2}
, X_{1}X_{2}X_{3}
, X_{2}X_{3}X_{4}
, X_{3}X_{4}X_{5}
, X_{4}X_{5}X_{6}
, X_{5}X_{6}X_{7}
, так как их углы \varphi
, \chi
, \psi
тупые, поэтому
\angle X_{0}OX_{1}+\angle X_{1}OX_{2}=\angle X_{0}OX_{2}=360^{\circ}-2\varphi=\angle X_{3}OX_{5}=\angle X_{3}OX_{4}+\angle X_{4}OX_{5},
\angle X_{1}OX_{2}+\angle X_{2}OX_{3}=\angle X_{1}OX_{3}=360^{\circ}-2\chi=\angle X_{4}OX_{6}=\angle X_{4}OX_{5}+\angle X_{5}OX_{6},
\angle X_{2}OX_{3}+\angle X_{3}OX_{4}=\angle X_{2}OX_{4}=360^{\circ}-2\psi=\angle X_{5}OX_{7}=\angle X_{5}OX_{6}+\angle X_{6}OX_{7}.
Имеем:
\angle X_{0}OX_{1}+3\cdot360^{\circ}-2\varphi-2\chi-2\psi=
=\angle X_{0}OX_{1}+(\angle X_{1}OX_{2}+\angle X_{2}OX_{3})+(\angle X_{3}OX_{4}+\angle X_{4}OX_{5})+(\angle X_{5}OX_{6}+\angle X_{6}OX_{7})=
=(\angle X_{0}OX_{1}+\angle X_{1}OX_{2})+(\angle X_{2}OX_{3}+\angle X_{3}OX_{4})+(\angle X_{4}OX_{5}+\angle X_{5}OX_{6})+\angle X_{6}OX_{7}=
=3\cdot360^{\circ}-2\varphi-2\chi-2\psi+\angle X_{6}OX_{7}.
Значит, \angle X_{0}OX_{1}=\angle X_{6}OX_{7}
, откуда следует равенство \rho_{1}=X_{0}X_{1}=X_{6}X_{7}=\rho_{7}
, равносильное r_{1}=r_{7}
. Что и требовалось.
Примечание. В условии задачи окружность \omega_{1}
выбирается произвольно. Для окружности \omega_{2}
, вписанной в угол B
и касающейся внешним образом \omega_{1}
, есть, вообще говоря, два варианта. Ровно как и для каждой из следующих четырёх окружностей. Причём «неправильный выбор» вариантов может дать цепочку окружностей, которая не замыкается. Именно чтобы избежать «неправильных цепочек», в условии сказано, что все окружности расположены внутри данного треугольника. Но это слишком сильное ограничение. Другие допустимые варианты расположения окружностей см. в п.3.1 статьи С.Дж.А.Ивлина, Г.Б.Мани-Каутса, Дж.А.Тиррелла «Теорема о семи окружностях и другие новые теоремы» (Математическое просвещение, 2019, выпуск 23, с. 51-79), являющейся переводом фрагмента книги C.J.A.Evelin, G.B.Money-Coutts, J.A.Tyrrell «The seven circles theorem and other new theorems» (London: Stacey Int., 1974).
Источник: «Математическое просвещение» (продолжающееся издание). — 2019, выпуск 23, с. 51-79
