13269. В треугольнике ABC
даны величины углов \angle B=12^{\circ}
, \angle C=132^{\circ}
(треугольник Боттемы). Проведены внешние биссектрисы BM
и CN
этих углов до пересечения с продолжениями противоположных сторон. Сравните длины этих биссектрис, не используя тригонометрические функции.
Ответ. Эти длины равны.
Решение. Пусть M
и N
— точки пересечения рассматриваемых внешних биссектрис с продолжениями противоположных сторон треугольника. Тогда
\angle BCM=180^{\circ}-132^{\circ}=48^{\circ},~\angle CBM=\frac{1}{2}(180^{\circ}-12^{\circ})=84^{\circ},
поэтому
\angle BMC=180^{\circ}-48^{\circ}-84^{\circ}=48^{\circ}=\angle BCM.
Значит, треугольник BMC
равнобедренный, BM=BC
, а так как по теореме о внешнем угле треугольника
\angle CAN=12^{\circ}+132^{\circ}=144^{\circ},
и при этом
\angle ACN=\frac{1}{2}\angle BCM=24^{\circ},
то
\angle ANC=180^{\circ}-144^{\circ}-24^{\circ}=12^{\circ}=\angle CBN.
Значит, треугольник BCN
тоже равнобедренный, CN=BC
. Следовательно, CN=BM
.
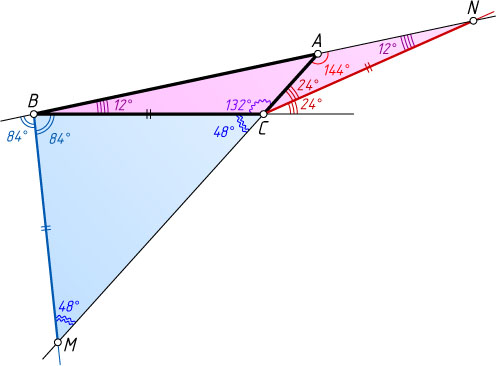
Примечание. Пример такого треугольника показывает, что для внешних биссектрис теорема, аналогичная теореме Штейнера-Лемуса (см. задачу 128), неверна.
Источник: Журнал «Mathematics Magazine». — 1974, том 47, № 1, задача 862, с. 52
Источник: Коксетер Г. С. М., Грейтцер С. Л. Новые встречи с геометрией. — М.: Наука, 1978. — № 1, с. 26
