13275. Вася нарисовал треугольник и отметил середины его сторон, основания высот и середины отрезков, соединяющих ортоцентр с вершинами. Некоторые из этих девяти точек могли совпасть — всего получилось k
различных точек. При каких k
могло оказаться, что эти точки являются вершинами правильного k
-угольника?
Ответ. 4, 6 и 8.
Решение. В любом треугольнике эти точки лежат на одной окружности — окружности девяти точек (см. задачу 174).
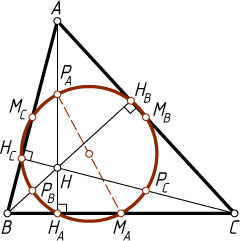
Пусть H
— ортоцентр разностороннего треугольника ABC
(рис. 1); H_{A}
, H_{B}
и H_{C}
— основания высот, проведённых из вершин A
, B
и C
соответственно; M_{A}
, M_{B}
и M_{C}
— середины сторон BC
, AC
и AB
соответственно; P_{A}
, P_{B}
и P_{C}
— середины отрезков AH
, BH
и CH
соответственно.
Поскольку \angle P_{A}H_{A}M_{A}=90^{\circ}
, отрезок P_{A}M_{A}
— диаметр окружности девяти точек. Это верно и в том случае, когда точки A_{M}
и H_{A}
совпадают — тогда треугольник ABC
равнобедренный и P_{A}M_{A}
— диаметр.
Итак, данный правильный k
-угольник вписан в окружность девяти точек и какие-то две из его вершин P_{A}
и M_{A}
в нём диаметрально противоположны. Следовательно, k
чётно.
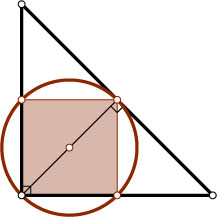
Для k=4
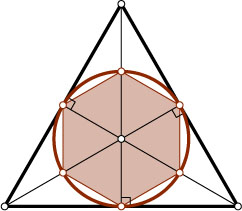
подходит равнобедренный прямоугольный треугольник (рис. 2), для k=6
— равносторонний треугольник (рис. 3). Докажем, что k=8
тоже подходит, т. е. приведём пример треугольника ABC
в котором восемь рассматриваемые точки — вершины правильного восьмиугольника.
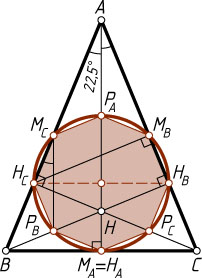
Пусть ABC
— равнобедренный треугольник с основанием BC
, причём \angle BAC=45^{\circ}
(рис. 4). Тогда точки H_{A}
и M_{A}
совпадают, а остальные попарно различны.
1. Все восемь точек лежат на одной окружности.
2. Этот восьмиугольник симметричен относительно прямой AH_{A}
, так как вся конструкция симметрична относительно этой прямой.
3. Отрезки P_{A}M_{A}
, P_{B}M_{B}
и P_{C}M_{C}
— диаметры, и H_{B}H_{C}
— тоже диаметр, так как
\angle H_{C}M_{B}H_{B}=\angle H_{C}M_{B}C=90^{\circ}
(медиана H_{C}M_{B}
равнобедренного треугольника AH_{C}C
является его высотой).
Таким образом, восьмиугольник симметричен относительно центра окружности. Значит, равны следующие дуги окружности девяти точек:
\smile P_{B}H_{C}=\smile P_{C}H_{B}=\smile M_{C}H_{C}=\smile M_{B}H_{B},
\smile P_{B}M_{A}=\smile P_{C}M_{A}=\smile M_{C}P_{A}=\smile M_{B}P_{A}.
Заметим, что из равенства дуг P_{A}M_{C}
и M_{A}P_{B}
следует параллельность хорд P_{B}M_{C}
и M_{A}P_{A}
, поэтому
\angle P_{B}M_{C}H_{C}=\angle HAH_{C}=\frac{1}{2}\angle BAC=\frac{1}{2}\cdot45^{\circ},
а так как центральный угол вдвое больше соответствующего вписанного, то
\smile P_{B}H_{C}=2\angle P_{B}M_{C}H_{C}=45^{\circ}.
Тогда каждая из дуг P_{B}H_{C}
, P_{C}H_{B}
, M_{C}H_{C}
и M_{B}H_{B}
равна 45^{\circ}
, их сумма равна 180^{\circ}
, а так как сумма всех восьми дуг равна 360^{\circ}
, то сумма равных дуг P_{B}M_{A}
, P_{C}M_{A}
, M_{C}P_{A}
и M_{B}P_{A}
тоже равна 180^{\circ}
. Значит, каждая из них равна 45^{\circ}
. Таким образом, все восемь дуг равны по 45^{\circ}
. Следовательно, эти восемь точек — вершины правильного многоугольника.
Примечание. 1. См. также статью И.Шарыгина и А.Ягубьянца «Окружность девяти точек и прямая Эйлера», Квант, 1981, N8, с.34.
4. См. также статью А.А.Заславского «Эйлер и геометрия», Квант, 2007, N3, с.37-40.