174. Докажите, что основания высот, середины сторон и середины отрезков от ортоцентра до вершин треугольника лежат на одной окружности (окружность девяти точек). Где расположен центр этой окружности?
Ответ. Середина отрезка OH
, где O
— центр описанной окружности треугольника, H
— ортоцентр.
Указание. Докажите сначала, что середины сторон треугольника и основание одной из высот лежат на одной окружности (или рассмотрите гомотетию с центром H
и коэффициентом \frac{1}{2}
).
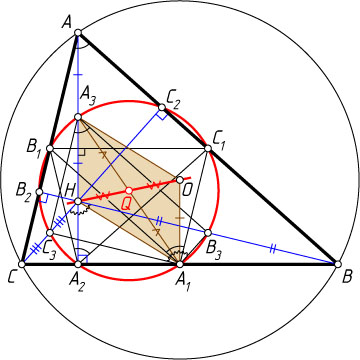
Решение. Первый способ. Пусть H
— точка пересечения высот (ортоцентр) треугольника ABC
; A_{1}
, B_{1}
, C_{1}
— середины сторон BC
, AC
, AB
соответственно; A_{2}
, B_{2}
, C_{2}
— основания высот, проведённых из вершин соответственно A
, B
, C
; A_{3}
, B_{3}
, C_{3}
— середины отрезков соответственно AH
, BH
, CH
.
Тогда C_{1}B_{1}
— серединный перпендикуляр к отрезку AA_{2}
. Поэтому
\angle C_{1}A_{2}B_{1}=\angle BAC=\angle C_{1}A_{1}B_{1}.
Следовательно, точки A_{2}
, A_{1}
, B_{1}
, C_{1}
лежат на одной окружности (отрезок C_{1}B_{1}
виден из точек A_{2}
и A_{1}
под одним и тем же углом).
Аналогично докажем, что точки B_{2}
, A_{1}
, B_{1}
, C_{1}
лежат на одной (той же) окружности, и точки C_{2}
, A_{1}
, B_{1}
, C_{1}
— на той же окружности.
Таким образом, точки A_{1}
, B_{1}
, C_{1}
, A_{2}
, B_{2}
, C_{2}
лежат на одной окружности.
Докажем теперь, что этой окружности принадлежат точки A_{3}
, B_{3}
, C_{3}
. Действительно, если углы B
и C
острые (рис. 1), то
\angle B_{3}A_{1}C_{3}=\angle BHC=180^{\circ}-\angle BAC=180^{\circ}-\angle B_{3}A_{3}C_{3}.
Если, например, угол B
тупой (рис. 2), то
\angle B_{3}A_{1}C_{3}=\angle BHC=\angle BAC=\angle B_{3}A_{3}C_{3}.
В любом из этих случаев точки A_{3}
, B_{3}
, A_{1}
, C_{3}
лежат на одной окружности.
Аналогично докажем, что на этой окружности лежат точки B_{1}
и C_{1}
. Следовательно, эта окружность совпадает с рассмотренной ранее.
Пусть O
— центр описанной окружности треугольника ABC
. Тогда OA_{1}=\frac{1}{2}AH=HA_{3}
(см. задачу 1257), а так как \angle A_{1}A_{2}A_{3}=90^{\circ}
, то A_{1}A_{3}
— диаметр окружности девяти точек.
Пусть Q
— точка пересечения диаметра A_{1}A_{3}
с отрезком OH
. Тогда Q
— точка пересечения диагоналей OH
и A_{1}A_{3}
параллелограмма OA_{1}HA_{3}
. Значит, Q
— общая середина отрезка OH
и диаметра A_{1}A_{3}
. Следовательно, центр окружности девяти точек — середина OH
.
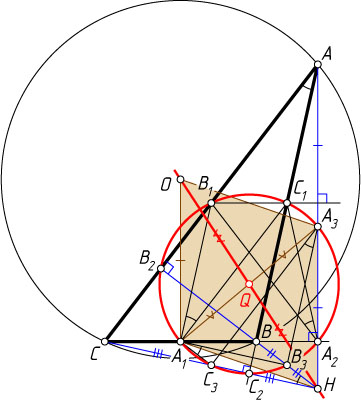
Второй способ. Пусть AA_{2}
, BB_{2}
и CC_{2}
— высоты треугольника ABC
(рис. 3). Поскольку точки, симметричные ортоцентру H
треугольника ABC
относительно его сторон, лежат на описанной окружности треугольника ABC
(см. задачу 4785), при гомотетии с центром H
и коэффициентом \frac{1}{2}
описанная окружность треугольника ABC
с центром O
переходит в описанную окружность треугольника A_{2}B_{2}C_{2}
. Центр этой окружности — середина отрезка OH
.
Вершины A
, B
и C
при этой гомотетии переходят в середины A_{3}
, B_{3}
и C_{3}
отрезков HA
, HB
и HC
соответственно, значит, эти точки лежат на описанной окружности треугольника A_{2}B_{2}C_{2}
.
Наконец, точки, симметричные ортоцентру треугольника относительно середин A_{1}
, B_{1}
и C_{1}
его сторон, лежат на описанной окружности треугольника ABC
(см. задачу 6300), значит, эти точки гомотетичны с коэффициентом \frac{1}{2}
и центром H
точкам, лежащим на описанной окружности треугольника ABC
, а следовательно, также лежат на описанной окружности треугольника A_{2}B_{2}C_{2}
.
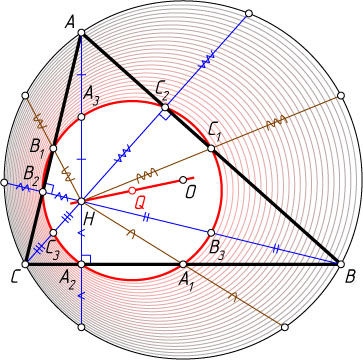
Третий способ. Пусть H
— точка пересечения высот (ортоцентр) треугольника ABC
; A_{1}
, B_{1}
, C_{1}
— середины сторон BC
, AC
, BC
соответственно; A_{2}
, B_{2}
, C_{2}
— основания высот, проведённых из вершин соответственно A
, B
, C
; A_{3}
, B_{3}
, C_{3}
— середины отрезков соответственно AH
, BH
, CH
.
Докажем сначала, что точки A_{1}
, A_{2}
, A_{3}
, B_{2}
и C_{2}
лежат на одной окружности.
Медианы B_{2}A_{3}
и C_{2}A_{3}
прямоугольных треугольников AB_{2}H
и AC_{2}H
равны половине общей гипотенузы AH
, поэтому B_{2}A_{3}=C_{2}A_{3}
. Медианы B_{2}A_{1}
и C_{2}A_{1}
прямоугольных треугольников BB_{2}C
и CC_{2}B
равны половине общей гипотенузы BC
, поэтому B_{2}A_{1}=C_{2}A_{1}
.
Обозначим \angle ACB=\gamma
. Тогда \angle CAA_{2}=90^{\circ}-\gamma
. Треугольники CA_{1}B_{2}
и AA_{3}B_{2}
равнобедренные, поэтому
\angle CB_{2}A_{1}=\angle A_{1}CB_{2}=\gamma,~\angle AB_{2}A_{3}=\angle B_{2}AA_{3}=90^{\circ}-\gamma.
Значит,
\angle A_{1}B_{2}A_{3}=180^{\circ}-\angle CB_{2}A_{1}-\angle AB_{2}A_{3}=180^{\circ}-\gamma-(90^{\circ}-\gamma)=90^{\circ}.
Аналогично, \angle A_{1}C_{2}A_{3}=90^{\circ}
. (Это рассуждение годится для остроугольного треугольника, но утверждение верно для любого треугольника.)
Пусть Q
— середина отрезка A_{1}A_{3}
. Медианы B_{2}Q
и C_{2}Q
прямоугольных треугольников A_{1}B_{2}A_{3}
и A_{1}C_{2}A_{3}
равны половине общей гипотенузы A_{1}A_{3}
, поэтому QB_{2}=QA_{3}=QA_{1}=QC_{2}
. Значит, точки A_{1}
, A_{3}
, B_{2}
и C_{2}
лежат на окружности с центром Q
и радиусом, равным половине отрезка A_{1}A_{3}
.
Осталось заметить, что QA_{2}
— медиана прямоугольного треугольника A_{1}A_{2}A_{3}
, проведённая к гипотенузе A_{1}A_{3}
. Следовательно, QA_{2}=\frac{1}{2}A_{1}A_{3}
, т. е. точка A_{2}
тоже лежит на этой окружности.
Таким образом, доказано, что середина A_{1}
стороны BC
и середина A_{3}
отрезка AH
лежат на окружности, проходящей через основания A_{2}
, B_{2}
и C_{2}
высот треугольника ABC
. Аналогично, на этой окружности лежат середины B_{1}
и C_{1}
сторон AC
и AB
, а также середины B_{3}
и C_{3}
отрезков BH
и CH
. Через три точки, не лежащие на одной прямой, проходит единственная окружность, следовательно, на ней лежат все девять рассматриваемых точек.
Осталось доказать, что Q
— середина отрезка OH
, где O
— центр описанной окружности треугольника ABC
. Прямая OA_{1}
— серединный перпендикуляр к стороне BC
треугольника ABC
, поэтому OA_{1}\parallel HA_{3}
. Кроме того, OA_{1}=HA_{3}
(см. задачу 1257). Следовательно, A_{3}HA_{1}O
— параллелограмм. Середина Q
его диагонали A_{1}A_{3}
совпадает с серединой его диагонали OH
. Что и требовалось доказать.
Примечание. 1. Предположим, что при решении первым способом уже доказана первая часть утверждения: окружность, проходящая через основания высот любого треугольника, проходит также через середины его сторон. Поскольку точки A_{1}
, B_{1}
и C_{1}
— основания высот треугольника BHC
, окружность, проходящая через эти точки, проходит также через середины его сторон BH
и CH
, т. е. через точки B_{3}
и C_{3}
. Отсюда следует утверждение задачи.
2. Из третьего способа доказательства следует, что прямые A_{1}B_{2}
и A_{1}C_{2}
— касательные к описанной окружности треугольника AB_{2}C_{2}
(так как A_{3}B_{2}\perp A_{1}B_{2}
и A_{3}C_{2}\perp A_{1}C_{2}
), а также, что AH=2OA_{1}
.
3. См. также статью И.Шарыгина и А.Ягубьянца «Окружность девяти точек и прямая Эйлера», Квант, 1981, N8.
4. См. также статью А.А.Заславского «Эйлер и геометрия», Квант, 2007, N3, с.37-40.
5. См. также статью Д.Швецова «Важная лемма», Квант, 2012, N5/6, с.57-60.
6. См. также пособие П.В.Бибикова, К.В.Козеренко, А.И.Малахова «Геометрия в сюжетах», 7-8 классы.
Источник: Яглом И. М. Геометрические преобразования. — Т. 1: Движения и преобразования подобия. — М.: ГИТТЛ, 1955. — № 51(а), с. 84
Источник: Ефремовъ Д. Д. Новая геометрiя треугольника. — Одесса, 1902. — с. 12
Источник: Пржевальский Е. Собрание геометрических теорем и задач. — М.: Типография Г. Лисснера и Д. Собко, 1909. — № 168 (фрагмент), с. 47
Источник: Адамар Ж. Элементарная геометрия. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1948. — № 101, с. 104
Источник: Вступительный экзамен в МФТИ. — 50, билет 14, № 4
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 50-14-4, с. 26
Источник: Кокстер Г. С. М. Введение в геометрию. — М.: Наука, 1966. — № 1.71, с. 36
Источник: Моденов П. С. Сборник задач по специальному курсу элементарной математики. — М.: Советская наука, 1957. — № 139, с. 193
Источник: Делоне Б. Н., Житомирский О. К. Задачник по геометрии. — М.—Л.: ОГИЗ, 1949. — № 88, с. 11
Источник: Задачи по математике и физике, дававшиеся на приёмных испытаниях в 1947—1953 гг. — М.: МФТИ, 1956. — № 48, с. 38
Источник: Шклярский Д. О., Ченцов Н. Н., Яглом И. М. Избранные задачи и теоремы элементарной математики. — Ч. 2: Геометрия (планиметрия). — М.: ГТТИ, 1952. — № 99, с. 32
Источник: Факультативный курс по математике: Учебное пособие для 7—9 кл. средней школы / Сост. И. Л. Никольская. — М.: Просвещение, 1991. — с. 97
Источник: Зетель С. И. Новая геометрия треугольника. — М.: Учпедгиз, 1962. — с. 53
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 457, с. 55
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 5.106, с. 118
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 5.129, с. 116
Источник: Шарыгин И. Ф., Голубев В. И. Факультативный курс по математике. Решение задач: Учебное пособие для 11 кл. средней школы. — М.: Просвещение, 1991. — № 371(а), с. 150
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — с. 212
Источник: Куланин Е. Д., Федин С. Н. Геометрия треугольника в задачах: Экспериментальное учебное пособие для 8—10 кл. школ физико-математического направления. — М.: НИИ школ, 1990. — № 53, с. 103


