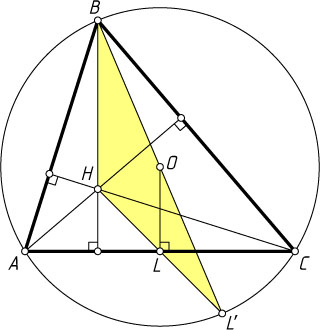
6300. Докажите, что образ ортоцентра треугольника при симметрии относительно середины стороны, лежит на описанной окружности треугольника.
Решение. Пусть H
— ортоцентр треугольника ABC
, L
— середина стороны AC
, O
— центр описанной окружности, L'
— точка пересечения прямых BO
и HL
.
Поскольку расстояние от ортоцентра треугольника до его вершины вдвое больше расстояния от центра описанной окружности до стороны, противоположной этой вершине (см. задачу 1257), OL=\frac{1}{2}BH
, а так как OL\parallel BH
, то OL
— средняя линия треугольника BHL'
. Значит, O
— середина отрезка BL'
. Следовательно, BL'
— диаметр окружности, т. е. точка L'
лежит на описанной окружности треугольника ABC
.
Примечание. Верно также следующее утверждение: если точка H
лежит на высоте треугольника ABC
, проведённой из вершины A
, а точка, симметричная A
относительно середины стороны BC
, лежит на описанной окружности треугольника ABC
, то H
— ортоцентр треугольника ABC
.
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — № 4.2, с. 42; № 1.11, с. 162
