4785. Докажите, что точки, симметричные точке пересечения высот (ортоцентру) треугольника ABC
относительно прямых, содержащих его стороны, лежат на описанной окружности этого треугольника.
Указание. Пусть H_{1}
— точка пересечения продолжения высоты AA_{1}
треугольника ABC
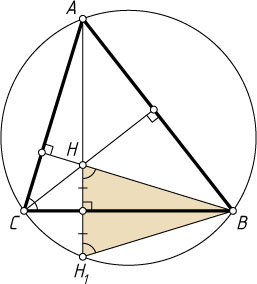
с описанной окружностью. Докажите, что треугольник HBH_{1}
— равнобедренный.
Решение. Для прямоугольного треугольника утверждение очевидно.
Пусть ABC
— остроугольный треугольник, H
— точка пересечения его высот, H_{1}
— точка пересечения продолжения отрезка AH
за точку H
с описанной окружностью треугольника ABC
. Тогда
\angle BH_{1}H=\angle BH_{1}A=\angle ACB=\angle BHH_{1}.
Поэтому треугольник HBH_{1}
— равнобедренный. Следовательно, перпендикуляр BC
к его стороне HH_{1}
проходит через середину отрезка HH_{1}
, т. е. точка H_{1}
симметрична точке H
относительно прямой BC
.
Аналогично проводится доказательство для тупоугольного треугольника.
Примечание. См. также задачу 5046.
Источник: Адамар Ж. Элементарная геометрия. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1948. — № 70, с. 82
Источник: Моденов П. С. Сборник задач по специальному курсу элементарной математики. — М.: Советская наука, 1957. — № 32, с. 184
Источник: Яглом И. М. Геометрические преобразования. — Т. 1: Движения и преобразования подобия. — М.: ГИТТЛ, 1955. — № 31(а), с. 46
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 5.9, с. 105
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 5.10, с. 103
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — № 4.2, с. 42; № 1.32, с. 168
Источник: Куланин Е. Д., Федин С. Н. Геометрия треугольника в задачах: Экспериментальное учебное пособие для 8—10 кл. школ физико-математического направления. — М.: НИИ школ, 1990. — № 50(1), с. 62
