1334. Пусть H
— точка пересечения высот треугольника ABC
. Докажите, что расстояние между серединами отрезков BC
и AH
равно радиусу описанной окружности треугольника ABC
.
Указание. Расстояние от точки пересечения высот треугольника до его вершины вдвое больше расстояния от центра описанной окружности до противолежащей стороны (см. задачу 1257).
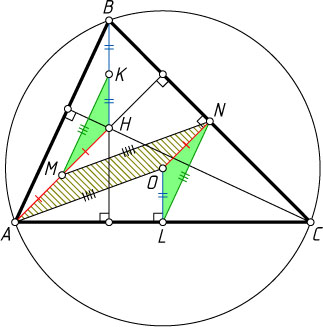
Решение. Пусть O
— центр описанной окружности треугольника ABC
, M
и N
— середины отрезков AH
и BC
соответственно. Докажем сначала, что AM=ON
. Для этого соединим точку M
с серединой K
отрезка BH
, а точку N
— с серединой L
отрезка AC
. Тогда MK
и NL
— средние линии треугольников ABH
и ABC
, поэтому MK=NL
и MK\parallel NL
, а так как HM\parallel ON
и HK\parallel OL
, то треугольники MHK
и NOL
равны по стороне и прилежащим к ней углам. Следовательно, ON=HM=AM
.
Поскольку ON=AM
и ON\parallel AM
, то четырёхугольник AMNO
— параллелограмм. Значит, MN=OA
. Осталось заметить, что OA
— радиус описанной окружности треугольника ABC
.
Источник: Пржевальский Е. Собрание геометрических теорем и задач. — М.: Типография Г. Лисснера и Д. Собко, 1909. — № 118, с. 42
Источник: Шарыгин И. Ф. Геометрия — 8. Теория и задачи: Экспериментальное учебное пособие для 8 кл. — М.: РОСТ, МИРОС, 1996. — № 8.1.21, с. 116
Источник: Куланин Е. Д., Федин С. Н. Геометрия треугольника в задачах: Экспериментальное учебное пособие для 8—10 кл. школ физико-математического направления. — М.: НИИ школ, 1990. — № 42, с. 61
