13442. В равносторонний треугольник вписаны две касающиеся окружности (см. рисунок). Найдите угол KLM
, где K
, L
и M
— точки касания.
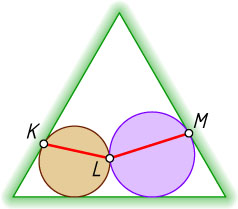
Ответ. 150^{\circ}
.
Решение. Пусть ABC
— данный равносторонний треугольник, O_{1}
и O_{2}
— центры данных окружностей.
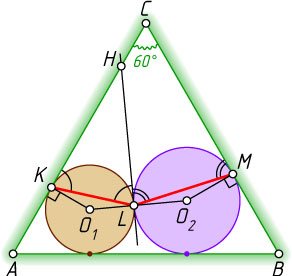
Проведём общую касательную LH
данных окружностей (рис. 1). Далее можно рассуждать по-разному.
Первый способ. Обозначим \angle KLH=\angle LKH=\alpha
. Тогда,
\angle HLM=\angle CML=90^{\circ}-\angle O_{2}ML=90^{\circ}-\angle O_{2}LM=
=90^{\circ}-\angle O_{1}LK=90^{\circ}-\angle O_{1}KL=\angle HKL=\alpha.
Сумма углов четырёхугольника CKLM
равна 360^{\circ}
, т. е.
60^{\circ}+4\alpha=360^{\circ},
откуда \alpha=75^{\circ}
. Следовательно, \angle KLM=2\alpha=150^{\circ}
.
Второй способ. Точка L
лежит на отрезке O_{1}O_{2}
(см. задачу 1759). Из пятиугольника CKO_{1}O_{2}M
находим, что сумма его углов при вершинах O_{1}
и O_{2}
равна
540^{\circ}-(60^{\circ}+90^{\circ}+90^{\circ})=300^{\circ}.
По теореме об угле между касательной и хордой получим
\angle KLM=\angle KLH+\angle MLH=\frac{1}{2}\angle KO_{1}L+\frac{1}{2}\angle MO_{2}L=
=\frac{1}{2}(\angle KO_{1}L+\angle MO_{2}L)=\frac{1}{2}\cdot300^{\circ}=150^{\circ}.
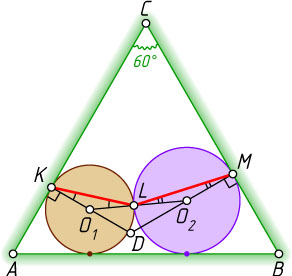
Примечание. Можно обойтись и без построения общей касательной. Достаточно продолжить радиусы O_{1}K
и O_{2}L
до пересечения в точке D
(рис. 2). Тогда из четырёхугольника CKDM
находим, что
\angle KDL=360^{\circ}-(60^{\circ}+90^{\circ}+90^{\circ})=120^{\circ}.
Значит, сумма углов при вершинах O_{1}
и O_{2}
треугольника O_{1}O_{2}D
равна 60^{\circ}
, а так как это внешние углы при вершинах равнобедренных треугольников KO_{1}L
и MO_{2}L
соответственно, то
\angle O_{1}LK+\angle O_{2}LM=30^{\circ},
откуда \angle KLM=150^{\circ}
.
Источник: Московская математическая регата. — 2022, задача 2.2, 9 класс


