13464. Окружности \omega_{1}
и \omega_{2}
касаются внутренним образом окружности \Omega
в различных точках A
и B
. Общая внешняя касательная к окружностям \omega_{1}
и \omega_{2}
касается их в точках D
и E
соответственно. Докажите, что прямые AD
и BE
пересекаются на окружности \Omega
.
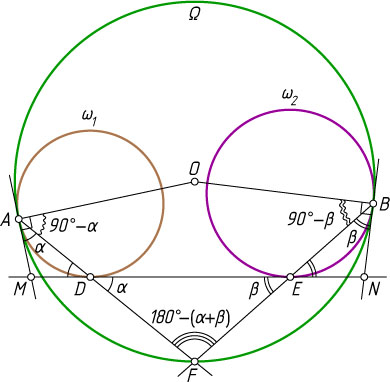
Решение. Рассмотрим случай, изображённый на рисунке. Для остальных случаев решение аналогично.
Пусть O
— центр окружности \Omega
, F
— точка пересечения прямых AD
и BE
, а прямая DE
пересекает в точках M
и N
касательные к окружности \Omega
, проведённые в точках A
и B
соответственно (и совпадающие с касательными к окружностям \omega_{1}
и \omega_{2}
в этих точках).
Обозначим \angle DAM=\alpha
, \angle EBN=\beta
. Тогда
\angle FDE=\angle ADM=\angle DAM=\alpha,
\angle FED=\angle BEN=\angle EBN=\beta,
\angle AFB=\angle DFE=180^{\circ}-(\alpha+\beta).
Поскольку AOB
— центральный угол окружности \Omega
, достаточно доказать, что не содержащая точку F
дуга AB
окружности \Omega
вдвое больше угла AFB
, т. е. равна 360^{\circ}-2(\alpha+\beta)
.
Действительно,
\angle OAF=\angle OAM-\angle DAM=90^{\circ}-\alpha,
\angle OBF=\angle OBN-\angle EBN=90^{\circ}-\beta.
Сумма углов четырёхугольника AFBO
равна 360^{\circ}
, т. е.
360^{\circ}=(90^{\circ}-\alpha)+(90^{\circ}-\beta)+(180^{\circ}-(\alpha+\beta))+\angle AOB,
откуда
\angle AOB=2(\alpha+\beta).
Следовательно, не содержащая точку F
дуга AB
окружности \Omega
равна 360^{\circ}-2(\alpha+\beta)
. Отсюда получаем утверждение задачи.
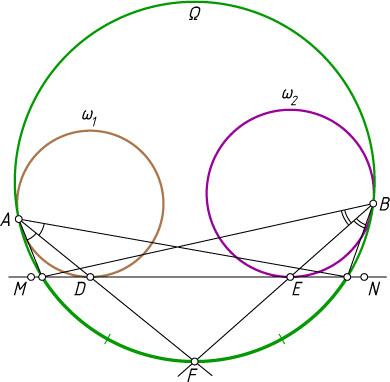
Примечание. По лемме Архимеда (см. задачу 89) лучи AD
и BE
проходят через середину дуги сегмента, отсекаемого от окружности \Omega
прямой MN
. Отсюда также следует утверждение задачи.
При таком рассуждении не нужен разбор случаев.
Источник: Журнал «Crux Mathematicorum». — 1997, № 8, задача 19, с. 461
Источник: Олимпиада «Baltic Way». — 1992

