13467. Пусть точка I
— центр вписанной окружности треугольника A_{1}A_{2}A_{3}
, точки I_{1}
, I_{2}
, I_{3}
— центры вневписанных окружностей, противолежащих вершинам A_{1}
, A_{2}
, A_{3}
соответственно, G
— точка пересечения медиан треугольника A_{1}A_{2}A_{3}
, H_{1}
— ортоцентр, треугольника I_{1}A_{2}A_{3}
. Аналогично определяются точки H_{2}
и H_{3}
. Докажите, что прямые A_{1}H_{1}
, A_{2}H_{2}
, A_{3}H_{3}
пересекаются в одной точке, причём эта точка лежит на прямой IG
.
Решение. Поскольку биссектрисы смежных углов перпендикулярны, точки A_{1}
, A_{2}
, A_{3}
лежат на сторонах треугольника I_{1}I_{2}I_{3}
и являются проекциями точки I
на стороны этого треугольника.
Поскольку A_{3}H_{1}\perp I_{1}I_{3}
и IA_{2}\perp I_{1}I_{3}
, то A_{3}H_{1}\parallel IA_{2}
. Аналогично, A_{2}H_{1}\parallel IA_{3}
. Значит, IA_{2}H_{1}A_{3}
— параллелограмм. Следовательно,
\overrightarrow{IH_{1}}=\overrightarrow{IA_{2}}+\overrightarrow{IA_{3}}.
Аналогично,
\overrightarrow{IH_{2}}=\overrightarrow{IA_{1}}+\overrightarrow{IA_{3}},~\overrightarrow{IH_{3}}=\overrightarrow{IA_{1}}+\overrightarrow{IA_{2}}.
Тогда
\frac{1}{2}(\overrightarrow{IA_{1}}+\overrightarrow{IH_{1}})=\frac{1}{2}(\overrightarrow{IA_{1}}+\overrightarrow{IA_{2}}+\overrightarrow{IA_{3}}),
\frac{1}{2}(\overrightarrow{IA_{2}}+\overrightarrow{IH_{2}})=\frac{1}{2}(\overrightarrow{IA_{2}}+\overrightarrow{IA_{1}}+\overrightarrow{IA_{3}}),
\frac{1}{2}(\overrightarrow{IA_{3}}+\overrightarrow{IH_{3}})=\frac{1}{2}(\overrightarrow{IA_{3}}+\overrightarrow{IA_{1}}+\overrightarrow{IA_{2}}).
Пусть точка S
— конец вектора \frac{1}{2}(\overrightarrow{IA_{1}}+\overrightarrow{IA_{2}}+\overrightarrow{IA_{3}})
. Тогда S
— общий конец векторов
\frac{1}{2}(\overrightarrow{IA_{1}}+\overrightarrow{IH_{1}}),~\frac{1}{2}(\overrightarrow{IA_{2}}+\overrightarrow{IH_{2}}),~\frac{1}{2}(\overrightarrow{IA_{3}}+\overrightarrow{IH_{3}}).
Это и означает, что прямые A_{1}H_{1}
, A_{2}H_{2}
, A_{3}H_{3}
пересекаются в одной точке — точке S
.
Поскольку (см. задачу 4505)
\overrightarrow{IG}=\frac{1}{3}(\overrightarrow{IA_{1}}+\overrightarrow{IA_{2}}+\overrightarrow{IA_{3}})~\mbox{и}~\overrightarrow{IS}=\frac{1}{2}(\overrightarrow{IA_{1}}+\overrightarrow{IA_{2}}+\overrightarrow{IA_{3}}),
то \overrightarrow{IG}=\frac{2}{3}\overrightarrow{IS}
. Следовательно, точка S
лежит на прямой IG
. Что и требовалось доказать.
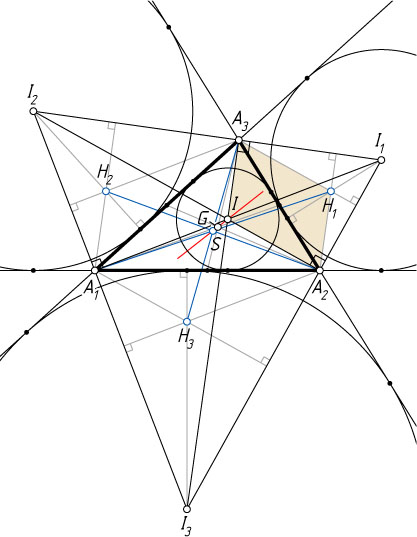
Источник: Журнал «Crux Mathematicorum». — 1990, № 2, задача 302 (1393)
