13525. Пусть P
и Q
— точки, лежащие внутри угла BAC
треугольника ABC
, причём прямая PQ
— серединный перпендикуляр к стороне BC
и \angle ABP+\angle ACQ=180^{\circ}
. Докажите, что \angle BAP=\angle CAQ
.
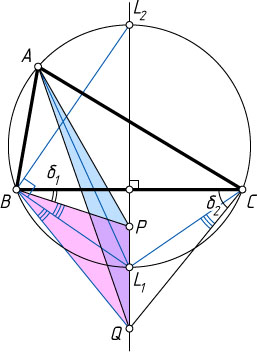
Решение. Первый способ. Рассмотрим случай, изображённый на рис. 1.
Пусть прямая PQ
пересекает описанную окружность треугольника ABC
в точках L_{1}
и L_{2}
Обозначим \angle BAC=\alpha
, \angle BAC=\beta
, \angle ACB=\gamma
, \angle CBP=\delta_{1}
, \angle BCQ=\delta_{2}
.
Тогда по условию
180^{\circ}=\angle ABP+\angle ACQ=(\beta+\delta_{1})+(\gamma+\delta_{2}),
откуда
\delta_{1}+\delta_{2}=180^{\circ}-\beta-\gamma=\alpha.
Значит, существует такое \delta
, что
\delta_{1}=\frac{\alpha}{2}-\delta,~\delta_{2}=\frac{\alpha}{2}+\delta.
Тогда
\angle L_{1}BQ=\angle L_{1}CQ=\angle BCQ-\angle BCL_{1}=
=\angle BCQ-\angle BAL_{1}=\delta_{2}-\frac{\alpha}{2}=\delta=\frac{\alpha}{2}-\delta_{1}=\angle PBL_{1}.
Следовательно, BL_{1}
— биссектриса треугольника BPQ
, а так как \angle L_{1}BL_{2}=90^{\circ}
, то BL_{2}
— внешняя биссектриса этого треугольника. Тогда окружность с диаметром L_{1}L_{2}
, т. е. описанная окружность треугольника ABC
, есть окружность Аполлония отрезка PQ
и отношения \frac{BP}{BQ}
(см. задачу 2444).
Точка L_{1}
лежит на этой окружности, поэтому \frac{L_{1}P}{L_{1}AQ}=\frac{BP}{BQ}=\frac{AP}{AQ}
. Значит, AL_{1}
— биссектриса угла PAQ
. В то же время, AL_{1}
— биссектриса угла BAC
, так как L_{1}
— середина дуги BL_{1}C
. Отсюда следует утверждение задачи.
Аналогично для остальных случаев.
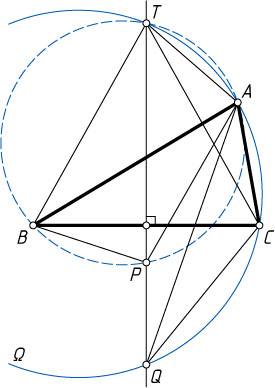
Второй способ. Рассмотрим случай, изображённый на рис. 2.
Пусть T
— отличная от Q
точка пересечения прямой PQ
с описанной окружностью \Omega
треугольника ACQ
. Тогда
\angle ATP=\angle ATQ=180^{\circ}-\angle ACQ=\angle ABP,
поэтому четырёхугольник ABPT
вписанный, и
\angle BAP=\angle BTP=\angle BTQ.
Поскольку PQ
— серединный перпендикуляр к отрезку BC
, то
\angle BTP=\angle CTP=\angle CAQ
(так как CTP
и CAQ
— углы вписанные в окружность \Omega
). Отсюда следует утверждение задачи.
Аналогично для остальных случаев.
Источник: Журнал «Crux Mathematicorum». — 1993, № 1, задача 1714 (44), с. 27

