13537. Три равные окружности проходят через одну точку и вторично пересекаются в точках A
, B
и C
. Треугольник A'B'C'
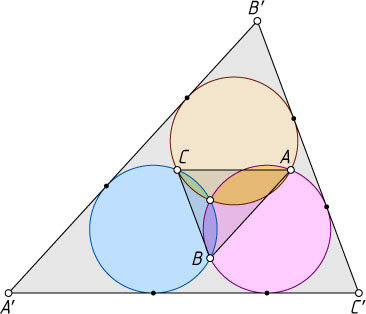
, содержит эти окружности, а каждая его сторона касается двух из них (см. рис.). Докажите, что S_{\triangle A'B'C'}\geqslant9S_{\triangle ABC}
.
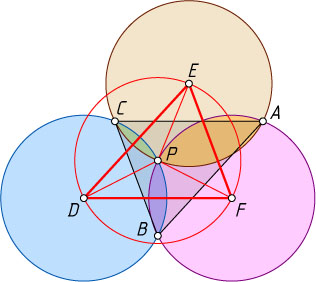
Решение. Пусть P
— общая точка трёх данных окружностей, а D
, E
и F
— их центры (рис. 1). Тогда P
— центр описанной окружности треугольника DEF
, так как расстояния от точки P
до точек D
, E
, F
равны радиусу данных окружностей.
Треугольники ABC
и DEF
равны (см. задачу 4620).
Пусть R
и r
— радиусы соответственно описанной и вписанной окружностей треугольников DEF
(и ABC
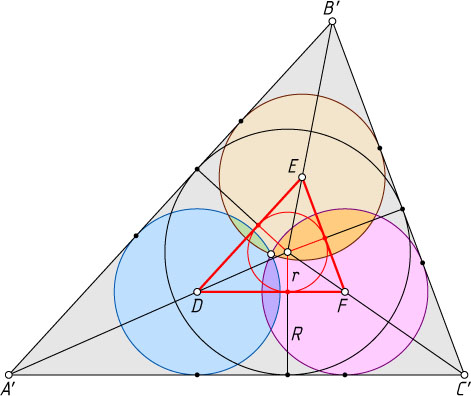
). Поскольку A'C'\parallel DF
, B'C'\parallel EF
и A'B'\parallel DE
, то расстояние между прямыми каждой пары равно R
(рис. 2). Кроме того, поскольку биссектрисы соответствующих углов треугольников A'B'C'
и DEF
лежат на одной прямой, то центры вписанных окружностей этих треугольников совпадают. Тогда радиус вписанной окружности треугольника A'B'C'
равен r+R
. Следовательно, коэффициент подобия треугольников A'B'C'
и DEF
равен \frac{R+r}{r}
, а так как R\geqslant2r
(см. задачу 3587), то
\frac{S_{\triangle A'B'C'}}{S_{\triangle ABC}}=\frac{S_{\triangle A'B'C'}}{S_{\triangle DEF}}=\left(\frac{R+r}{r}\right)^{2}\geqslant\left(\frac{2r+r}{r}\right)^{2}=9.
Что и требовалось доказать.
Источник: Журнал «Crux Mathematicorum». — 1993, № 10, задача 1808 (16), с. 299


