13543. Проведены четыре общих касательных к двум окружностям (см. рисунок). Докажите, что расстояние между параллельными прямыми AG
и CX
равно расстоянию между параллельными прямыми DY
и FH
.
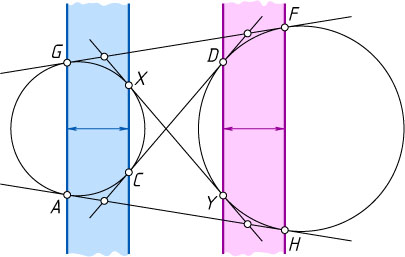
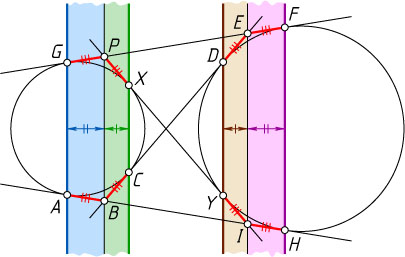
Решение. Введём обозначения, как показано на рисунке. Отрезки AB
, BC
, ED
, EF
, IH
, IY
, XP
, PG
равны (см. задачу 4805), причём проекции отрезков AB
, IH
, EF
, PG
на линию центров равны, так как касательные, на которых расположены эти отрезки, образуют с линией центров равные углы. Аналогично, равны проекции отрезков BC
, XP
, ED
, IY
.
Расстояние между параллельными прямыми AG
и CX
равно сумме проекций отрезков AB
и BC
, а расстояние между параллельными прямыми DY
и FH
равно сумме проекций отрезков IY
и IH
. Следовательно, эти расстояния равны.
Источник: Журнал «Crux Mathematicorum». — 1994, № 5, задача 1858 (170), с. 149

