13548. На продолжениях сторон треугольника ABC
отложены отрезки BC_{1}=CB_{2}=BC
, CA_{1}=AC_{2}=CA
и AB_{1}=BA_{2}=AB
, как показано на рисунке. Докажите, что площадь шестиугольника A_{1}C_{2}B_{1}A_{2}C_{1}B_{2}
минимальна, если треугольник ABC
равносторонний.
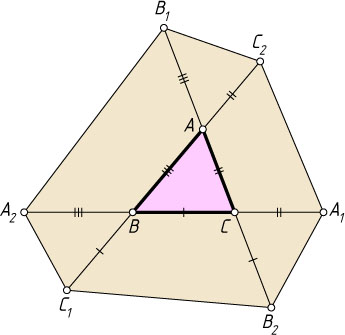
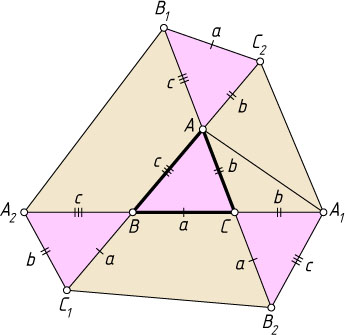
Решение. Заметим, что треугольники ABC
, AB_{1}C_{2}
, A_{2}BC_{1}
и A_{1}B_{2}C
равны по двум сторонам и углу между ними.
Обозначим
BC_{1}=CB_{2}=BC=a,~CA_{1}=AC_{2}=CA=b,~AB_{1}=BA_{2}=AB=c.
Отношение площадей треугольников с равными высотами равно отношению оснований этих треугольников, поэтому
\frac{S_{\triangle BAA_{1}}}{S_{\triangle ABC}}=\frac{a+b}{a},~\frac{S_{\triangle A_{1}BC_{2}}}{S_{\triangle BAA_{1}}}=\frac{b+c}{c}.
Перемножив эти равенства, получим
\frac{S_{\triangle A_{1}BC_{2}}}{S_{\triangle ABC}}=\frac{(a+b)(b+c)}{ac}.
Аналогично,
\frac{S_{\triangle A_{2}B_{1}C}}{S_{\triangle ABC}}=\frac{(b+c)(a+c)}{ab},~\frac{S_{\triangle AB_{2}C_{1}}}{S_{\triangle ABC}}=\frac{(a+b)(a+c)}{bc}.
Заметим, что,
S_{A_{1}C_{2}B_{1}A_{2}C_{1}B_{2}}=S_{\triangle A_{1}BC_{2}}+S_{\triangle A_{2}B_{1}C}+S_{\triangle AB_{2}C_{1}}+S_{\triangle ABC},
поэтому
\frac{S_{A_{1}C_{2}B_{1}A_{2}C_{1}B_{2}}}{S_{\triangle ABC}}=1+\frac{(a+b)(b+c)}{ac}+\frac{(b+c)(a+c)}{ab}+\frac{(a+b)(a+c)}{bc}=
=4+\left(\frac{b}{a}+\frac{a}{b}\right)+\left(\frac{b}{c}+\frac{c}{b}\right)+\left(\frac{c}{a}+\frac{a}{c}\right)+\left(\frac{b^{2}}{ac}+\frac{c^{2}}{ab}+\frac{a^{2}}{bc}\right)\geqslant
\geqslant4+2+2+2+3\sqrt[{3}]{{\frac{b^{2}}{ac}\cdot\frac{c^{2}}{ab}\cdot\frac{a^{2}}{bc}}}\geqslant4+2+2+2+3=13
(см. задачу 3399), причём равенство достигается в случае, если a=b=c
, т. е. когда треугольник ABC
равносторонний. Что и требовалось доказать.
Примечание. Кроме того, доказано неравенство S_{A_{1}C_{2}B_{1}A_{2}C_{1}B_{2}}\geqslant13S_{\triangle ABC}
.
Источник: Журнал «Crux Mathematicorum». — 1994, № 8, задача 1887 (265), с. 236

