13549. Дан равнобедренный треугольник ABC
(AB=AC
). Точка D
— основание перпендикуляра, опущенного из точки C
на прямую AB
, точка M
— середина отрезка CD
, E
— основание перпендикуляра, опущенного из вершины A
на прямую BM
, F
— основание перпендикуляра, опущенного из вершины A
на прямую CE
. Докажите, что AF\leqslant\frac{1}{3}AB
.
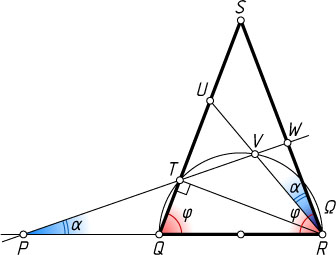
Решение. Лемма. На основании QR
равнобедренного треугольника SQR
как на диаметре построена полуокружность \Omega
, пересекающая сторону SQ
в точке T
. Прямая, проведённая через точку T
, пересекает прямую QR
и сторону SR
в точках P
и W
, а полуокружность \Omega
— вторично в точке V
. Прямая RV
пересекает сторону SQ
в точке U
. Тогда \frac{QU}{US}=2\frac{PQ}{QR}
.
Доказательство. Обозначим \angle TPR=\alpha
, \angle SQR=\angle SRQ=\varphi
(рис. 1). Тогда по теореме о внешнем угле треугольника \angle PTQ=\varphi-\alpha
, а так как четырёхугольник QTWR
вписанный, то
\angle SRU=\angle SRQ-\angle VRQ=\angle SRQ-(180^{\circ}-\angle VTQ)=
=\angle SRQ-\angle PTQ=\varphi-(\varphi-\alpha)=\alpha.
Применив теорему синусов и учитывая, что \angle QTR=90^{\circ}
, получим
\frac{PQ}{QR}=\frac{\frac{PQ}{QT}}{\frac{QR}{QT}}=\frac{\frac{\sin(\varphi-\alpha)}{\sin\alpha}}{\frac{1}{\cos\varphi}}=\frac{\sin(\varphi-\alpha)\cos\varphi}{\sin\alpha},
\frac{QU}{US}=\frac{\frac{QU}{UR}}{\frac{US}{UR}}=\frac{\frac{\sin(\varphi-\alpha)}{\sin\varphi}}{\frac{\sin\alpha}{\sin(180^{\circ}-2\varphi)}}=\frac{\sin(\varphi-\alpha)\sin2\varphi}{\sin\varphi\sin\alpha}=\frac{2\sin(\varphi-\alpha)\cos\varphi}{\sin\alpha}.
Следовательно, \frac{QU}{US}=2\frac{PQ}{QR}
. Лемма доказана.
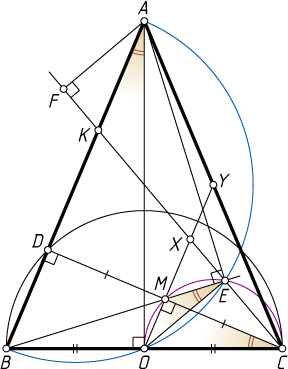
Вернёмся к нашей задаче. Пусть O
— середина отрезка BC
, прямая OM
пересекает отрезки CF
и AC
в точках X
и Y
соответственно, а K
— точка пересечения прямой CF
с боковой стороной AB
(рис. 2).
Поскольку OM
— средняя линия треугольника BCD
, то по теореме Фалеса Y
— середина боковой стороны AC
, и OY\parallel AB
.
Из точек O
и E
отрезок AB
виден под прямым углом, значит, эти точки лежат на окружности с диаметром AB
. Тогда
\angle MEO=\angle BEO=\angle BAO=\angle BCD=\angle OCM.
Следовательно, точки O
, M
, E
и C
лежат на одной окружности, а так как \angle OMC=\angle BDC=90^{\circ}
, отрезок OC
— диаметр этой окружности. Таким образом, для треугольника YOC
выполнены все условия леммы, поэтому
\frac{YX}{XO}=\frac{1}{2}\cdot\frac{BO}{OC}=\frac{1}{2},
т. е. XY=\frac{1}{3}OY
, а так как OY\parallel AB
, то AK=\frac{1}{3}AB
(см. задачу 1597). Следовательно, из прямоугольного треугольника AFK
получаем, что AF\leqslant\frac{1}{3}AB
. Что и требовалось доказать.
Источник: Журнал «Crux Mathematicorum». — 1994, № 9, задача 1761, с. 251

