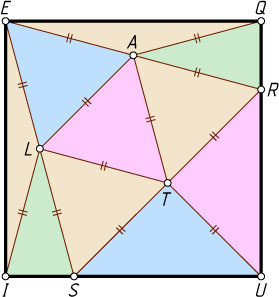
13598. Разбейте квадрат на треугольники так, чтобы все стороны треугольников, расположенные внутри квадрата, были равны и были меньше стороны квадрата.
Решение. Отметим внутри квадрата EQUI
точки A
, L
и T
из условия задачи 13597. Тогда ALE
, ALT
— равносторонние треугольники, а отрезки LI
, AQ
и UT
равны сторонам этих треугольников. Обозначим их через a
.
Пусть R
— точка пересечения продолжения отрезка EA
со стороной QU
квадрата. Тогда ER
— диаметр описанной окружности прямоугольного треугольника EQR
, а так как AE=AQ
, то точка A
отрезка ER
лежит на серединном перпендикуляре к стороне EQ
этого треугольника. Значит, A
— центр окружности, и AR=AQ=AE=a
.
Кроме того, ET
— биссектриса угла AEL
ромба AELT
, а так как \angle IEL=\angle QEA
, то EL
— биссектриса угла AEL
(и ATL
). Тогда \angle AET=30^{\circ}
, а так как AT=AE=AR
, то точка T
лежит на рассматриваемой окружности, \angle ETR=90^{\circ}
и TR=\frac{1}{2}ER=AR=a
.
Аналогично, если S
— точка пересечения продолжения EL
со стороной IU
квадрата, то TS=SL=a
. Таким образом, все 12 отрезков разбиения равны и, очевидно, меньше стороны квадрата.
Источник: Журнал «Crux Mathematicorum». — 1997, № 8, задача H216, с. 495
